题目内容
3.数列{an}满足an+1=$\left\{\begin{array}{l}2{a_n},0≤{a_n}≤\frac{1}{2}\\ 2{a_n}-1,\frac{1}{2}<{a_n}<1\end{array}$,a1=$\frac{3}{5}$,Sn为{an}的前n项和,则S2016=1008.分析 计算数列{an}的前几项即可发现数列的周期,从而得出S2016.
解答 解:a1=$\frac{3}{5}$,a2=2a1-1=$\frac{1}{5}$,a3=2a2=$\frac{2}{5}$,a4=2a3=$\frac{4}{5}$,a5=2a4-1=$\frac{3}{5}$,
∴{an}为周期为4的摆动数列,
∴S2016=(a1+a2+a3+a4)×$\frac{2016}{4}$=2×504=1008.
故答案为:1008.
点评 本题考查了分段函数的函数求值,数列求和,属于基础题.

练习册系列答案
相关题目
3.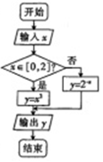 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
 如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )
如图是函数y=f(x)求值的程序框图,若输出函数y=f(x)的值域为[4,8],则输入函数y=f(x)的定义域不可能为( )| A. | [-3,-2] | B. | [-3,-2)∪{2} | C. | [-3,2] | D. | [-3,-2]∪{2} |
18.已知集合P={1,2,3,4,5},Q={X∈R|2≤X≤5},那么下面结论正确的是( )
| A. | P∪Q=P | B. | P∩Q?Q | C. | P∪Q=Q | D. | P∩Q⊆P |
15.将函数f(x)=sinωx-cosωx+1(ω>0)的图象向左平移$\frac{π}{4}$个单位,再向下平移1个单位,得到函数y=g(x)的图象,若y=g(x)的相邻两个零点之差的绝对值等于$\frac{π}{2}$,则函数y=g(x)的一个单调递减区间是( )
| A. | [0,$\frac{π}{8}$] | B. | [$\frac{π}{8}$,π] | C. | [$\frac{π}{4}$,$\frac{3π}{4}$] | D. | [$\frac{π}{8}$,$\frac{5π}{8}$] |
13.函数$y=tan({\frac{π}{2}-x})$$x∈[{-\frac{π}{4},\frac{π}{4}}]$且x≠0的值域为( )
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,1) | D. | [-1,+∞) |