题目内容
17.已知向量$\overrightarrow m=(sinx,-1)$,向量$\overrightarrow n=(\sqrt{3}cosx,-\frac{1}{2})$,函数$f(x)=(\overrightarrow m+\overrightarrow n)•\overrightarrow m$.(1)求f(x)的解析式及单调增区间;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=2$\sqrt{3}$,c=4,且f(A)恰是f(x)在$[{0,\frac{π}{2}}]$上的最大值,求A,b和△ABC的面积S.
分析 (1)利用向量的数量积运算结合降幂公式及辅助角公式即可求得f(x)的解析,再由复合函数的单调性求得函数的单调区间;
(2)求出f(x)在$[{0,\frac{π}{2}}]$上的最大值,得到A的值,利用正弦定理求得C,进一步得到B,再由面积公式求得△ABC的面积.
解答 解:(1)∵$\overrightarrow m=(sinx,-1)$,$\overrightarrow n=(\sqrt{3}cosx,-\frac{1}{2})$,
∴函数$f(x)=(\overrightarrow m+\overrightarrow n)•\overrightarrow m$=(sinx+$\sqrt{3}cosx$,$-\frac{3}{2}$)•(sinx,-1)
=sinx(sinx+$\sqrt{3}cosx$)+$\frac{3}{2}$=$si{n}^{2}x+\sqrt{3}sinxcosx+\frac{3}{2}$
=$\frac{1-cos2x}{2}+\frac{\sqrt{3}}{2}sin2x+\frac{3}{2}$=$\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x+2$
=sin(2x-$\frac{π}{6}$)+2.
由$-\frac{π}{2}+2kπ≤2x-\frac{π}{6}≤\frac{π}{2}+2kπ$,k∈Z.
得$-\frac{π}{6}+kπ≤x≤\frac{π}{3}+kπ$,k∈Z.
∴f(x)的单调增区间为[$-\frac{π}{6}+kπ$,$\frac{π}{3}+kπ$];
(2)∵x∈$[{0,\frac{π}{2}}]$,∴2x$-\frac{π}{6}$∈[$-\frac{π}{6}$,$\frac{5π}{6}$].
则f(x)在$[{0,\frac{π}{2}}]$上的最大值为3.
即f(A)=3,∴sin(2A-$\frac{π}{6}$)+2=3,2A-$\frac{π}{6}$=$\frac{π}{2}$,得A=$\frac{π}{3}$.
又a=2$\sqrt{3}$,c=4,
∴由$\frac{2\sqrt{3}}{sin\frac{π}{3}}=\frac{4}{sinC}$,得sinC=1,∴C=$\frac{π}{2}$.
则B=$π-\frac{π}{2}-\frac{π}{3}=\frac{π}{6}$.
∴△ABC的面积S=$\frac{1}{2}ac•sinB=\frac{1}{2}×2\sqrt{3}×4×\frac{1}{2}=2\sqrt{3}$.
点评 本题考查三角函数中的恒等变换应用,考查三角函数的图象和性质,考查三角形的解法,是中档题.

| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
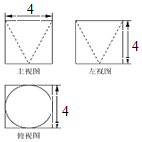
| A. | $8-\frac{2π}{3}$ | B. | $64-\frac{16π}{3}$ | C. | $8-\frac{π}{3}$ | D. | $64-\frac{12π}{3}$ |
 如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18km,速度为1 000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1km,参考数据:$\sqrt{3}$≈1.732)( )
如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18km,速度为1 000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1km,参考数据:$\sqrt{3}$≈1.732)( )| A. | 11.4 km | B. | 6.6 km | C. | 6.5 km | D. | 5.6 km |

| A. | 20 | B. | 50 | C. | 140 | D. | 150 |
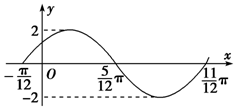 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的一段图象如图所示.
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的一段图象如图所示.