题目内容
求证：
=
．
| 1+sin4θ-cos4θ |
| 2tanθ |
| 1+sin4θ+cos4θ |
| 1-tan2θ |
考点：三角函数恒等式的证明
专题：三角函数的求值
分析：由分析法一步步把要证明的式子转化为二倍角的正切公式，从而使问题得证．
解答：
解：要证
=
，
只需证
=
，
即证
=
，
即证
=
，即证
=
，
只需证tan2θ=
，
由二倍角的正切公式可知上式正确，
故原命题得证．
| 1+sin4θ-cos4θ |
| 2tanθ |
| 1+sin4θ+cos4θ |
| 1-tan2θ |
只需证
| 1+2sin2θcos2θ-(1-2sin22θ) |
| 2tanθ |
| 1+2sin2θcos2θ+2cos22θ-1 |
| 1-tan2θ |
即证
| 2sin2θ(sin2θ+cos2θ) |
| 2tanθ |
| 2cos2θ(sin2θ+cos2θ) |
| 1-tan2θ |
即证
| sin2θ |
| 2tanθ |
| cos2θ |
| 1-tan2θ |
| sin2θ |
| cos2θ |
| 2tanθ |
| 1-tan2θ |
只需证tan2θ=
| 2tanθ |
| 1-tan2θ |
由二倍角的正切公式可知上式正确，
故原命题得证．
点评：本题考查三角函数恒等式的证明，涉及二倍角公式和分析法证明恒等式，属中档题．
练习册系列答案
相关题目
已知 如图，四边形ABCD是等腰梯形，AB∥DC，A（-1，-2），B（6，5），D（0，2）．
在长方体ABCD-A1B1C1D1中，AB=AD=3，AA1=4，E为AA1的中点．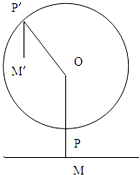
六一儿重节到了，小明与爸爸去游乐场看见了大观览车，已知大观览车轮轴中心为点O，距地面高为32m（即OM=32m），巨轮半径为30m，点p为吊舱与轮的连接点，吊舱高2m（即PM=2m）巨轮每分钟转动30°，小明和爸爸从地面M点进入吊舱后，巨轮开始逆时针转动．