题目内容
已知数列{an}的前n项和Sn=-an-(
)n-1+2(n∈N*),数列{bn}满足bn=2nan,
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(2)设数列{
an}的前n项和为Tn,证明:n∈N*且n≥3时Tn>
.
| 1 |
| 2 |
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(2)设数列{
| n+1 |
| n |
| 5n |
| 2n+1 |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)利用“当n≥2时,an=Sn-Sn-1”及其等差数列的通项公式即可得出.
(2)利用错位相减法求和,即可证明结论.
(2)利用错位相减法求和,即可证明结论.
解答:
证明:(1)a1=
,当n≥2时,an=Sn-Sn-1,
∴2an=an-1+(
)n-1,即2nan=2n-1an-1+1,
∴bn=bn-1+1,又b1=2a1=1,
∴{bn}是首项和公差均为1的等差数列.
∴bn=n=2nan,∴an=
(2)由(1)得
an=(n+1)(
)n,
∵Tn=2×
+3×(
)2+…+(n+1)(
)n,
∴
Tn=2×(
)2+3×(
)3+…+(n+1)(
)n+1,
∴
Tn=2-
,
∴Tn=4-
,
证明n∈N*且n≥3时,4-
>
n=3时,左边=8,右边=
;
设n=k时,结论成立,即4-
>
.
则n=k+1时,4-
>
+
-
>
∴n=k+1时,结论成立
综上,n∈N*且n≥3时Tn>
.
| 1 |
| 2 |
∴2an=an-1+(
| 1 |
| 2 |
∴bn=bn-1+1,又b1=2a1=1,
∴{bn}是首项和公差均为1的等差数列.
∴bn=n=2nan,∴an=
| n |
| 2n |
(2)由(1)得
| n+1 |
| n |
| 1 |
| 2 |
∵Tn=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| n+5 |
| 2n+1 |
∴Tn=4-
| n+5 |
| 2n |
证明n∈N*且n≥3时,4-
| n+5 |
| 2n |
| 5n |
| 2n+1 |
n=3时,左边=8,右边=
| 15 |
| 7 |
设n=k时,结论成立,即4-
| k+5 |
| 2k |
| 5k |
| 2k+1 |
则n=k+1时,4-
| k+6 |
| 2k+1 |
| 5k |
| 2k+1 |
| k+5 |
| 2k |
| k+6 |
| 2k+1 |
| 5(k+1) |
| 2k+3 |
∴n=k+1时,结论成立
综上,n∈N*且n≥3时Tn>
| 5n |
| 2n+1 |
点评:本题综合考查了“当n≥2时,an=Sn-Sn-1”及其等差数列的通项公式、“错位相减法”等基础知识与基本方法,正确求通项与数列的和是关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
等比数列{an},满足an>0,2a1+a2=a3,则公比q=( )
| A、1 | B、2 | C、3 | D、4 |
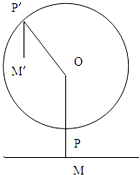 六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.
六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.