题目内容
已知函数f(x)=loga(3-ax)(a>0,a≠1)
(1)求函数f(x)的定义域;
(2)若函数f(x)在[2,6]上递增,并且最小值为loga(
),求实数a的值.
(1)求函数f(x)的定义域;
(2)若函数f(x)在[2,6]上递增,并且最小值为loga(
| 7 |
| 9a |
考点:对数函数的图像与性质,对数函数的定义域
专题:函数的性质及应用
分析:(1)根据对数函数的定义,即可求出定义域,
(2)根据函数复合函数的单调性即可得到a的值.
(2)根据函数复合函数的单调性即可得到a的值.
解答:
解:(1)∵f(x)=loga(3-ax),
∴3-ax>0,
即x<
∴函数f(x)的定义域为x∈(-∞,
),
(2)f(x)在[2,6]上递增,最小值为loga(
),
∴由题意得f(2)=loga
,
则loga(3-2a)=loga
解得a=
或
,
又
,
则a=
舍去,
所以a=
.
∴3-ax>0,
即x<
| 3 |
| a |
∴函数f(x)的定义域为x∈(-∞,
| 3 |
| a |
(2)f(x)在[2,6]上递增,最小值为loga(
| 7 |
| 9a |
∴由题意得f(2)=loga
| 7 |
| 9a |
则loga(3-2a)=loga
| 7 |
| 9a |
解得a=
| 1 |
| 3 |
| 7 |
| 6 |
又
|
则a=
| 7 |
| 6 |
所以a=
| 1 |
| 3 |
点评:本题主要考查对数函数的性质,以及复合函数的单调性,属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
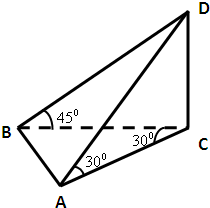 如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔
如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔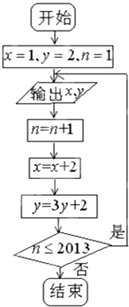 根据如图的程序框图,将输出的x,y值依次分别记为x1,x2,…,x2013;y1,y2…y2013
根据如图的程序框图,将输出的x,y值依次分别记为x1,x2,…,x2013;y1,y2…y2013