题目内容
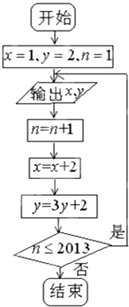根据如图的程序框图，将输出的x，y值依次分别记为x1，x2，…，x2013；y1，y2…y2013（Ⅰ）写出数列{xn}，{yn}的通项公式（不要求写出求解过程）；
（Ⅱ）求Sn=x1（y1+1）+x2（y2+1）+…+xn（yn+1）（n≤2013）．
考点：程序框图
专题：计算题,算法和程序框图
分析：循环体中x=x+2，y=3y+2是数列的递推公式变形，从而求出通项公式，（2）错位相减法求和．
解答：
解：（Ⅰ）由题意，数列{xn}，{yn}的通项公式为
xn=2n-1，yn=3n-1，（n≤2013）．
（Ⅱ）Sn=x1（y1+1）+x2（y2+1）+…+xn（yn+1）
=1×31+3×32+5×33+…+（2n-1）3n，
3Sn=1×32+3×33+5×34+…+（2n-1）3n+1，
则2Sn=（2n-1）3n+1-3-2（32+33+34+…+3n），
∴Sn=（n-1）3n+1+3（n≤2013）．
xn=2n-1，yn=3n-1，（n≤2013）．
（Ⅱ）Sn=x1（y1+1）+x2（y2+1）+…+xn（yn+1）
=1×31+3×32+5×33+…+（2n-1）3n，
3Sn=1×32+3×33+5×34+…+（2n-1）3n+1，
则2Sn=（2n-1）3n+1-3-2（32+33+34+…+3n），
∴Sn=（n-1）3n+1+3（n≤2013）．
点评：本题考查了程序框图的应用，及错位相减法，属于中档题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目