题目内容
已知函数f(x)=2sin2x+
sin2x-1.
(1)求函数f(x)的零点;
(2)若方程f(x-
)+4sinx+1=a在x∈[
,
]上有解,求实数a的取值范围.
| 3 |
(1)求函数f(x)的零点;
(2)若方程f(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
考点:三角方程,函数的零点
专题:三角函数的求值
分析:(1)f(x)=2sin(2x-
),令2x-
=kπ,得x=
+
,由此能求出f(x)的零点.
(2)由已知得a=4(sinx+
)2-2,由此利用已知条件能推导出a∈[2,7].
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
| kπ |
| 2 |
(2)由已知得a=4(sinx+
| 1 |
| 2 |
解答:
解:(1)f(x)=1-cos2x+
sin2x-1=2(sin2xcos
-cos2xsin
)=2sin(2x-
)
令:2x-
=kπ,得x=
+
,所以f(x)的零点为x=
+
(2)a=f(x-
)+4sinx+1=2sin(2x-
-
)+4sinx+1=-2cos2x+4sinx+1
=-2(1-2sin2x)+4sinx+1
=4sin2x+4sinx-1
=4(sinx+
)2-2
当x∈[
,
]时,sinx∈[
,1],4(sinx+
)2-2∈[2,7]
因为f(x-
)+4sinx=a在x∈[
,
]上有解,所以a∈[2,7]
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
令:2x-
| π |
| 6 |
| π |
| 12 |
| kπ |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
(2)a=f(x-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
=-2(1-2sin2x)+4sinx+1
=4sin2x+4sinx-1
=4(sinx+
| 1 |
| 2 |
当x∈[
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为f(x-
| π |
| 12 |
| π |
| 6 |
| π |
| 2 |
点评:本题考查函数的零点的求法,考查实数的取值范围的求法,解题时要注意三角函数性质的合理运用.

练习册系列答案
相关题目
 已知f(x)=2cos2x+2
已知f(x)=2cos2x+2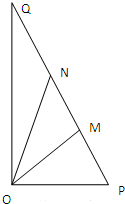 某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40
某房地产项目打造水景工程,拟在小区绿地中建设人工湖.该绿地形状为Rt△OPQ(如图),∠POQ=90°,OP=40m,OQ=40