题目内容
4.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,且过点$({1,\frac{{\sqrt{3}}}{2}})$.(1)求E的方程;
(2)若直线l:y=kx+m(k>0)与E相交于P,Q两点,且OP与OQ(O为坐标原点)的斜率之和为2,求O到直线l距离的取值范围.
分析 (1)由椭圆离心率及点在椭圆上,列式计算,求出a2,b2,即可得椭圆E的方程.
(2)把y=kx+m代入E的方程得:(1+4k2)x2+8kmx+4(m2-1)=0,其判别式△=16(4k2-m2+1)>0,设P(x1,y1),Q(x2,y2),由已知得${k_{OF}}+{k_{OQ}}=\frac{y_1}{x_1}+\frac{y_2}{x_2}=\frac{{{y_1}{x_2}+{y_2}{x_1}}}{{{x_1}{x_2}}}=\frac{{({k{x_1}+m}){x_2}+({k{x_2}+m}){x_1}}}{{{x_1}{x_2}}}=2$,2(k-1)x1x2+m(x1+x2)=0,即m2+k=1,0<k≤1,点O到直线l的距离为d,当k=1时,d=0;当k≠1时$d=\frac{|m|}{{\sqrt{{k^2}+1}}}=\frac{1}{{\sqrt{\frac{{{k^2}+1}}{m^2}}}}=\frac{1}{{\sqrt{\frac{{{k^2}+1}}{1-k}}}}$,令1-k=t∈(0,1),利用函数单调性可得点O到直线l的距离的取值范围
解答 解:(1)由已知得$\frac{c}{a}=\frac{{\sqrt{3}}}{2},\frac{1}{a^2}+\frac{3}{{4{b^2}}}=1$,
解得a2=4,b2=1,∴椭圆E的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)把y=kx+m代入E的方程得:(1+4k2)x2+8kmx+4(m2-1)=0,
其判别式△=16(4k2-m2+1)>0,①
设P(x1,y1),Q(x2,y2),
则${x_1}+{x_2}=\frac{-8km}{{1+4{k^2}}},{x_1}{x_2}=\frac{{4({{m^2}-1})}}{{1+4{k^2}}}$,②
由已知得${k_{OF}}+{k_{OQ}}=\frac{y_1}{x_1}+\frac{y_2}{x_2}=\frac{{{y_1}{x_2}+{y_2}{x_1}}}{{{x_1}{x_2}}}=\frac{{({k{x_1}+m}){x_2}+({k{x_2}+m}){x_1}}}{{{x_1}{x_2}}}=2$,
∴2(k-1)x1x2+m(x1+x2)=0,③
把②代入③得$\frac{{8({k-1})({{m^2}-1})}}{{1+4{k^2}}}-\frac{{8k{m^2}}}{{1+4{k^2}}}=0$,
即m2+k=1,④
把④代入①及k>0知4k2+k>0,
又m2=1-k≥0,∴0<k≤1,
点O到直线l的距离为d,
当k=1时,d=0;
当k≠1时,$d=\frac{|m|}{{\sqrt{{k^2}+1}}}=\frac{1}{{\sqrt{\frac{{{k^2}+1}}{m^2}}}}=\frac{1}{{\sqrt{\frac{{{k^2}+1}}{1-k}}}}$,
令1-k=t∈(0,1),则$d=\frac{1}{{\sqrt{t+\frac{2}{t}-2}}}$,
设$y=t+\frac{2}{t}-2$,则$y'=1-\frac{2}{t^2}=\frac{{{t^2}-2}}{t^2}<0$,∴$y=t+\frac{2}{t}-2$在(0,1)单调递减,
∴当t∈(0,1)时,d∈(0,1),
综上,点O到直线l的距离的取值范围为[0,1).
点评 本题考查了椭圆的方程,直线与椭圆的位置关系,距离公式,同时考查了函数与方程思想及运算能力,属于难题.

 小题狂做系列答案
小题狂做系列答案| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
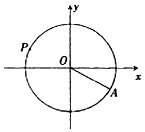 水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )
水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3$\sqrt{3}$,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<$\frac{π}{2}}$).则下列叙述错误的是( )| A. | $R=6,ω=\frac{π}{30},φ=-\frac{π}{6}$ | |
| B. | 当t∈[35,55]时,点P到x轴的距离的最大值为6 | |
| C. | 当t∈[10,25]时,函数y=f(t)单调递减 | |
| D. | 当t=20时,$|{PA}|=6\sqrt{3}$ |
| A. | 4 | B. | 17 | C. | 28 | D. | 41 |
| A. | (-∞,0)∪(0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |

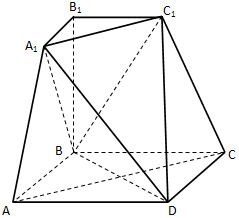 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.