题目内容
在数列{an}中,a1=1,an+1=
(n∈N+),试写出这个数列的前4项,并猜想这个数列的通项公式,并给以证明.
| 2an |
| 2+an |
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:根据数列的递推公式,计算出数列{an}的前4项,猜想出通项公式,并用数学归纳法证明.
解答:
解:数列{an}中,∵a1=1,an+1=
(n∈N+),
∴a2=
=
=
,
a3=
=
=
,
a4=
=
=
,…;
猜想数列{an}的通项公式为an=
,n∈N*;
用数学归纳法证明:
当n=1时,a1=
=1,满足条件;
假设n=k时,ak=
成立,
则n=k+1时,ak+1=
=
=
,也满足条件;
∴数列{an}的通项公式为an=
,n∈N*.
| 2an |
| 2+an |
∴a2=
| 2a1 |
| 2+a1 |
| 2×1 |
| 2+1 |
| 2 |
| 3 |
a3=
| 2a2 |
| 2+a2 |
2×
| ||
2+
|
| 1 |
| 2 |
a4=
| 2a3 |
| 2+a3 |
2×
| ||
2+
|
| 2 |
| 5 |
猜想数列{an}的通项公式为an=
| 2 |
| n+1 |
用数学归纳法证明:
当n=1时,a1=
| 2 |
| 2 |
假设n=k时,ak=
| 2 |
| k+1 |
则n=k+1时,ak+1=
| 2ak |
| 2+ak |
=
2×
| ||
2+
|
=
| 2 |
| k+2 |
∴数列{an}的通项公式为an=
| 2 |
| n+1 |
点评:本题考查了数列的递推公式以及计算数列的项和猜想归纳推论能力,解题时可用数学归纳法证明,是综合题.

练习册系列答案
相关题目
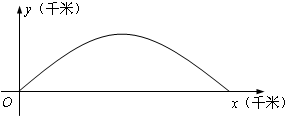 如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-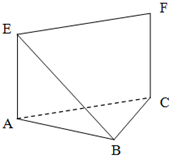 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.