题目内容
9.已知命题p:实数m满足:方程$\frac{{x}^{2}}{m-3a}$+$\frac{{y}^{2}}{m-4a}$=1(a>0)表示双曲线;命题q:实数m满足方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{2-m}$=1表示焦点在y轴上的椭圆,且?p是?q的必要不充分条件,求实数a的取值范围.分析 求出命题p、q是真命题时m的取值范围,再根据¬p是¬q的必要不充分条件得出¬q是¬p的充分不必要条件,从而求出a的取值范围.
解答 解:若方程$\frac{{x}^{2}}{m-3a}$+$\frac{{y}^{2}}{m-4a}$=1(a>0)表示双曲线,
则有(m-3a)(m-4a)<0(a>0),
解得3a<m<4a;
由方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{2-m}$=1表示焦点在y轴上的椭圆,
则有2-m>m-1>0,
解得1<m<$\frac{3}{2}$;
由¬p是¬q的必要不充分条件,∴可知¬q是¬p的充分不必要条件,
即$\left\{\begin{array}{l}{3a≥1}\\{4a≤\frac{3}{2}}\end{array}\right.$,
从而解得$\frac{1}{3}$≤a≤$\frac{3}{8}$.
点评 本题利用充分、必要条件考查了椭圆与双曲线的标准方程的应用问题,也考查了不等式的解法与应用问题,是基础题目.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{kx-2,x>0}\\{-ln(-x),x<0}\end{array}\right.$ 的图象上有两对关于坐标原点对称的点,则实数k的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{e}$) | C. | (0,+∞) | D. | (0,e) |
4.已知函数$f(x)=\left\{\begin{array}{l}x(x-1),x>0\\{log_3}(1-x),x≤0\end{array}\right.$,若f(m)=2,则实数m的值为( )
| A. | -1或2 | B. | -8或-1 | C. | -8或2 | D. | -8,-1或2 |
1.某中药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材品质,基地收益如下表所示:
若基地额外聘请工人,可在周一当天完成全部采摘任务;无雨时收益为20万元;有雨时收益为10万元,额外聘请工人的成本为a万元.已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为20万元的概率为0.36.(1)若不额外聘请工人,写出基地收益X的分布列及基地的预期收益;
(2)该基地是否应该外聘工人,请说明理由.
| 周一 | 无雨 | 无雨 | 有雨 | 有雨 |
| 周二 | 无雨 | 有雨 | 无雨 | 有雨 |
| 收益 | 20万 | 15万 | 10万 | 7.5万 |
(2)该基地是否应该外聘工人,请说明理由.
19.已知函数f(x)=kx-1,其中实数k随机选自区间[-1,2].则对任意的x∈[-1,1],f(x)≤0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
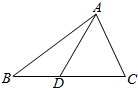 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.