题目内容
18.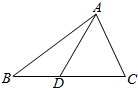 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.(Ⅰ)求cosC;
(Ⅱ)求线段AD的长.
分析 (Ⅰ)由已知根据余弦定理可得$cosC=\frac{{A{C^2}+B{C^2}-A{B^2}}}{2AC•BC}$代入计算即可得解.
(Ⅱ)由0<C<π,可得sinC>0,从而可求sinC的值,利用正弦定理即可求得AD的值.
解答 (本小题共13分)
解:(Ⅰ)∵AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,
∴根据余弦定理:$cosC=\frac{{A{C^2}+B{C^2}-A{B^2}}}{2AC•BC}$=$\frac{{{{(3\sqrt{6})}^2}+{{(5\sqrt{6})}^2}-{{12}^2}}}{{2•3\sqrt{6}•5\sqrt{6}}}=\frac{1}{3}$.…(6分)
(Ⅱ)∵0<C<π,
∴sinC>0,$sinC=\sqrt{1-{{cos}^2}C}=\sqrt{1-{{(\frac{1}{3})}^2}}=\frac{{2\sqrt{2}}}{3}$.
∴根据正弦定理得:$\frac{AD}{sinC}=\frac{AC}{sin∠ADC}$,即:$AD=\frac{AC•sinC}{sin∠ADC}$=8.…(13分)
点评 本题主要考查了余弦定理,正弦定理,同角三角函数基本关系式的综合应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
13.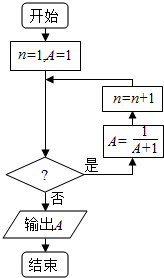 已知数列{an}中,${a_1}=1,{a_{n+1}}=\frac{1}{{1+{a_n}}}$,若利用下面程序框图计算该数列的第2016项,则判断框内的条件是( )
已知数列{an}中,${a_1}=1,{a_{n+1}}=\frac{1}{{1+{a_n}}}$,若利用下面程序框图计算该数列的第2016项,则判断框内的条件是( )
 已知数列{an}中,${a_1}=1,{a_{n+1}}=\frac{1}{{1+{a_n}}}$,若利用下面程序框图计算该数列的第2016项,则判断框内的条件是( )
已知数列{an}中,${a_1}=1,{a_{n+1}}=\frac{1}{{1+{a_n}}}$,若利用下面程序框图计算该数列的第2016项,则判断框内的条件是( )| A. | n≤2014 | B. | n≤2016 | C. | n≤2015 | D. | n≤2017 |
10.已知角θ满足sinθ-2cosθ=0,则$\frac{{cos(\frac{3π}{2}+θ)+4cos(π-θ)}}{{sin(\frac{π}{2}-θ)-sin(π-θ)}}$=( )
| A. | -2 | B. | 0 | C. | $\frac{2}{3}$ | D. | 2 |
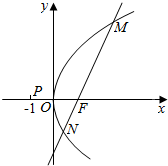 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.