已知数列{an}的通项为an=$\frac{1}{cosncos(n+1)}$(n∈N*).求其前n项和Sn．题目和参考答案——青夏教育精英家教网——

题目内容

14．已知数列{a_n}的通项为a_n=$\frac{1}{cosncos（n+1）}$（n∈N^*），求其前n项和S_n．

分析由$\frac{sin1}{cosncos（n+1）}$=$\frac{sin（n+1-n）}{cosncos（n+1）}$=tan（n+1）-tann，可得a_n=$\frac{1}{sin1}$[tan（n+1）-tann]，即可得出．

解答解：由$\frac{sin1}{cosncos（n+1）}$=$\frac{sin（n+1-n）}{cosncos（n+1）}$=$\frac{sin（n+1）cosn-cos（n+1）sinn}{cosncos（n+1）}$=tan（n+1）-tann，
∴a_n=$\frac{1}{cosncos（n+1）}$=$\frac{1}{sin1}$[tan（n+1）-tann]，
∴其前n项和S_n=$\frac{1}{sin1}$[（tan2-tan1）+（tan3-tan2）+…+tan（n+1）-tann]
=$\frac{1}{sin1}$[tan（n+1）-tan1]．

点评本题考查了数列的通项公式及其前n项和公式、“裂项求和”方法、和差化积、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

尖子生单元测试系列答案

轻松假期行暑假用书系列答案

世纪百通主体课堂小学课时同步练习系列答案

经纶学典棒棒堂系列答案

全程导航大提速系列答案

课程导学系列答案

Top巅峰特训系列答案

新课堂新坐标高三一轮总复习系列答案

百年学典全优课堂高考总复习系列答案

新课标高考总复习创新方案系列答案

相关题目

14．对于函数f（x），若存在区间M=[a，b]，使得{y|y=f（x），x∈M}=M，则称函数f（x）具有性质P，给出下列3个函数：
①f（x）=sinx；
②f（x）=x³-3x；
③f（x）=lgx+3．
其中具有性质P的函数是②．（填入所有满足条件函数的序号）

15．已知tan（α-$\frac{π}{4}$）=2，则$\frac{sin2α-co{s}^{2}α}{1+cos2α}$的值为$\frac{1}{2}$．

2．已知a=1.7^-2.5，b=2.5^1.7，c=${log_2}{\frac{2}{3}}$，则a，b，c的大小关系为（　　）

9．已知命题p：实数m满足：方程$\frac{{x}^{2}}{m-3a}$+$\frac{{y}^{2}}{m-4a}$=1（a＞0）表示双曲线；命题q：实数m满足方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{2-m}$=1表示焦点在y轴上的椭圆，且?p是?q的必要不充分条件，求实数a的取值范围．

19．设数列{a_n}的前n项和为S_n，a₁=1，a₂=3，a₃=5且（2n+1）S_n+1-（2n+5）S_n=An+B，n∈N^*，其中A，B为常数．
（1）求A，B的值；
（2）证明：数列{a_n}为等差数列；
（3）数列{a_n}中是否存在两项a_m、a_k（m，k∈N^*），使得${a}_{k}^{4}$-2a_k+22=${a}_{m}^{2}$，如果存在，求出所有的k和m，如果存在，请说明理由．

6．已知点${A}（{0，2\sqrt{2}}）$，抛物线y²=2px（p＞0）的焦点为F，线段F A的中点B在抛物线上，若抛物线在点B处的切线与x轴交于点C，则△BFC的面积为$\frac{3\sqrt{2}}{4}$．

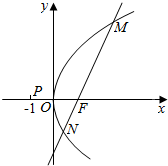已知点F为抛物线C：y²=2px（p＞0）的焦点，过点F的动直线l与抛物线C交于M，N两点，如图．当直线l与x轴垂直时，|MN|=4．
（Ⅰ）求抛物线C的方程；
（Ⅱ）已知点P（-1，0），设直线PM的斜率为k₁，直线PN的斜率为k₂．请判断k₁+k₂是否为定值，若是，写出这个定值，并证明你的结论；若不是，说明理由．

4．已知集合A={1，2，3}，B={2，3，4，5}，全集U={1，2，3，4，5，6}，则∁_U（A∩B）=（　　）

{1，4，5，6}

{1，2，3，4，5}