题目内容
8.已知函数$f(x)=\left\{\begin{array}{l}|{log_2}x|,x>0\\-{x^2}-2x,x≤0\end{array}\right.$,关于x的方程f(x)=m(m∈R)有四个不同的实数解x1,x2,x3,x4则x1x2x3x4的取值范围为(0,1).分析 作函数$f(x)=\left\{\begin{array}{l}|{log_2}x|,x>0\\-{x^2}-2x,x≤0\end{array}\right.$的图象,从而可得x3x4=1,推出x1x2的范围即可求解结果.
解答  解:作函数$f(x)=\left\{\begin{array}{l}|{log_2}x|,x>0\\-{x^2}-2x,x≤0\end{array}\right.$的图象如下,
解:作函数$f(x)=\left\{\begin{array}{l}|{log_2}x|,x>0\\-{x^2}-2x,x≤0\end{array}\right.$的图象如下,
结合图象可知,-log2x3=log2x4,
故x3x4=1,
令-x2-2x=0得,x=0或x=-2,
令-x2-2x=1得,x=-1;
故x1x2∈(0,1),
故x1x2x3x4∈(0,1).
故答案为:(0,1).
点评 本题考查了数形结合的思想应用及学生的作图能力,同时考查了配方法的应用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
18.一个底面积为1的正四棱柱的顶点都在同一球面上,若此球的表面积为20π,则该四棱柱的高为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3$\sqrt{2}$ | D. | $\sqrt{19}$ |
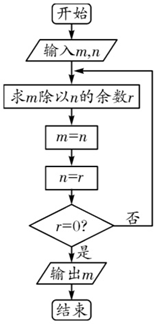 阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为24.
阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为24.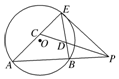 如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证:
如图,A,B,E是⊙O上的点,过E点的⊙O的切线与直线AB交于点P,∠APE的平分线和AE,BE分别交于点C,D.求证: