题目内容
18．一个底面积为1的正四棱柱的顶点都在同一球面上，若此球的表面积为20π，则该四棱柱的高为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | 3$\sqrt{2}$ | D． | $\sqrt{19}$ |
分析 根据球的表面积公式，可算出R，由正四棱柱的顶点在同一球面上，可得正四棱柱体对角线恰好是球的一条直径，即可得出结论．
解答 解：根据球的表面积公式，得此球的表面积为S=4πR2=20π，∴R=$\sqrt{5}$．
∵正四棱柱的底面积为1，
∴正四棱柱的底面边长为1，
∵正四棱柱的顶点在同一球面上，
∴正四棱柱体对角线恰好是球的一条直径，
∴2$\sqrt{5}$=$\sqrt{1+1+{h}^{2}}$，∴h=3$\sqrt{2}$，
故选C．
点评 本题考查球的表面积，考查了正四棱柱的性质、长方体对角线公式和球的表面积公式等知识，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
8．已知集合A={x∈N|3-2x＞0}，B={x|x2≤4}，则A∩B=（ ）
| A． | {x|-2≤x＜1} | B． | {x|x≤2} | C． | {0，1} | D． | {1，2} |
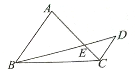如图所示，AC与BD交于点E，AB∥CD，AC=3$\sqrt{5}$，AB=2CD=6，当tanA=2时，$\overrightarrow{BE}•\overrightarrow{DC}$=-12．
13．若复数z-i=1+i，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{5}$ | D． | 5 |
3．二项式$（x-\frac{2}{x}{）^6}$的展开式的第二项是（ ）
| A． | 6x4 | B． | -6x4 | C． | 12x4 | D． | -12x4 |