题目内容
11.若实数x,y满足$\left\{\begin{array}{l}x-y≤1\\ x-2y+2≥0\\ 2x+y≥2\end{array}\right.$则z=x-ay只在点(4,3)处取得最大值,则a的取值范围为( )| A. | (-∞,0)∪(1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (-∞,1) |
分析 由约束条件作出可行域,然后对a进行分类,当a≥0时显然满足题意,当a<0时,化目标函数为直线方程斜截式,比较其斜率与直线BC的斜率的大小得到a的范围.
解答 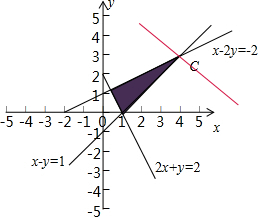 解:由不等式组$\left\{\begin{array}{l}x-y≤1\\ x-2y+2≥0\\ 2x+y≥2\end{array}\right.$作可行域如图,
解:由不等式组$\left\{\begin{array}{l}x-y≤1\\ x-2y+2≥0\\ 2x+y≥2\end{array}\right.$作可行域如图,
联立$\left\{\begin{array}{l}{x-2y=-2}\\{x-y=1}\end{array}\right.$,解得C(4,3).
当a=0时,目标函数化为z=x,由图可知,
可行解(4,3)使z=x-ay取得最大值,符合题意;
当a>0时,由z=x-ay,得y=$\frac{1}{a}$x$-\frac{z}{a}$,此直线斜率大于0,当在y轴上截距最大时z最大,
可行解(4,3)为使目标函数z=x-ay的最优解,
a<1符合题意;
当a<0时,由z=x-ay,得y=$\frac{1}{a}$x$-\frac{z}{a}$,此直线斜率为负值,
要使可行解(4,3)为使目标函数z=x-ay取得最大值的唯一的最优解,则$\frac{1}{a}$<0,即a<0.
综上,实数a的取值范围是(-∞,1).
故选:D.
点评 本题考查线性规划问题,考查了分类讨论的数学思想方法和数形结合的解题思想方法,解答的关键是化目标函数为直线方程斜截式,由直线在y轴上的截距分析z的取值情况,是中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
6.已知点(a,b)是圆x2+y2=r2外的一点,则直线ax+by=r2与圆的位置关系 ( )
| A. | 相离 | B. | 相切 | C. | 相交且不过圆心 | D. | 相交且过圆心 |
16.已知f(x)=$\frac{(x+2)^{0}}{x+1}$,则f(x)的定义域是( )
| A. | {x|x≠-2} | B. | {x|x≠-1} | C. | {x|x≠-1且x≠-2} | D. | {x|x≠-1或x≠-2} |
3.在平面直角坐标系中,若点P(m-3,m+1)在第二象限,则m的取值范围为( )
| A. | -1<m<3 | B. | m>3 | C. | m<-1 | D. | m>-1 |