题目内容
6.已知点(a,b)是圆x2+y2=r2外的一点,则直线ax+by=r2与圆的位置关系 ( )| A. | 相离 | B. | 相切 | C. | 相交且不过圆心 | D. | 相交且过圆心 |
分析 由点(a,b)是圆x2+y2=r2外的一点,知a2+b2<r2,由此得到 圆心(0,0)到直线ax+by=r2的距离d∈(0,r),由此能判断直线ax+by=r2与圆的位置关系.
解答 解:∵点(a,b)是圆x2+y2=r2外的一点,
∴a2+b2<r2,
∵圆心(0,0)到直线ax+by=r2的距离:
d=$\frac{|-{r}^{2}|}{\sqrt{{a}^{2}+{b}^{2}}}$<r,且d>0,
∴直线ax+by=r2与圆相交且不过圆心.
故选:C.
点评 本题考查直线与圆的位置关系的判断,考查点到直线的距离公式的应用,是基础题,解题时要认真审题,注意圆、直线方程等知识点的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若实数x,y满足$\left\{\begin{array}{l}x-y≤1\\ x-2y+2≥0\\ 2x+y≥2\end{array}\right.$则z=x-ay只在点(4,3)处取得最大值,则a的取值范围为( )
| A. | (-∞,0)∪(1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (-∞,1) |
15.函数$f(x)=sin(x+\frac{π}{4})cos(x+\frac{π}{4})+{cos^2}x-{log_2}|x|-\frac{1}{2}$的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.如果直线y=2x-1和y=kx互相垂直,则实数k的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
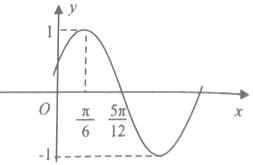 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,