题目内容
20.设Sn是数列{an}的前n项和(n∈N*),若a1=1,Sn-1+Sn=3n2+2(n≥2),则S101=15451.分析 当n≥2时,Sn-1+Sn=3n2+2,Sn+Sn+1=3(n+1)2+2,可得an+1+an=6n+3.利用等差数列的前n项和公式即可得出.
解答 解:当n≥2时,Sn-1+Sn=3n2+2,Sn+Sn+1=3(n+1)2+2,可得an+1+an=6n+3,
∴S101=a1+(a2+a3)+(a4+a5)+…+(a100+a101)
=1+(6×2+3)+(6×4+3)+…+(6×100+3)
=1+$\frac{50(15+603)}{2}$
=15451.
故答案为:15451.
点评 本题考查了递推式的应用、等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
11.若实数x,y满足$\left\{\begin{array}{l}x-y≤1\\ x-2y+2≥0\\ 2x+y≥2\end{array}\right.$则z=x-ay只在点(4,3)处取得最大值,则a的取值范围为( )
| A. | (-∞,0)∪(1,+∞) | B. | (1,+∞) | C. | (0,1) | D. | (-∞,1) |
8.已知i是虚数单位,若$\frac{1+2i}{z}$=2-i,则z的模为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | i | D. | 1 |
15.函数$f(x)=sin(x+\frac{π}{4})cos(x+\frac{π}{4})+{cos^2}x-{log_2}|x|-\frac{1}{2}$的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.若圆(x-1)2+(y-4)2=4的圆心到直线ax+y-1=0的距离为1,则a=( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
10.若$sinx=-\frac{1}{4}$,$x∈({π\;,\;\;\frac{3π}{2}})$,则( )
| A. | $x=arcsin({-\frac{1}{4}})$ | B. | $x=-arcsin\frac{1}{4}$ | C. | $x=π+arcsin\frac{1}{4}$ | D. | $x=π-arcsin\frac{1}{4}$ |
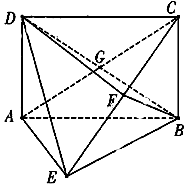 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为线段CE上一点,且BF⊥平面ACE,AC交BD于点G.