题目内容
在一次研究性学习中,老师给出函数f(x)=
(x∈R),三位同学甲、乙、丙在研究此函数时
给出命题:你认为上述三个命题中正确的个数有( )
甲:函数f(x)的值域为(-1,1);乙:若x1≠x2,则一定有f(x1)≠f(x2);
丙:若规定f1(x)=f(x),fn(x)=f(fn-1(x)),则fn(x)≥
对任意n∈N*恒成立.
| x |
| 1+|x| |
给出命题:你认为上述三个命题中正确的个数有( )
甲:函数f(x)的值域为(-1,1);乙:若x1≠x2,则一定有f(x1)≠f(x2);
丙:若规定f1(x)=f(x),fn(x)=f(fn-1(x)),则fn(x)≥
| x |
| 1+n|x| |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:甲:利用函数的奇偶性单调性即可得出;
乙:利用导数研究函数的单调性即可得出;
丙:利用函数的奇偶性、数学归纳法即可得出.
乙:利用导数研究函数的单调性即可得出;
丙:利用函数的奇偶性、数学归纳法即可得出.
解答:
解:甲:由函数f(x)=
(x∈R),当x≥0时,f(x)=
,∴0≤f(x)<1;∵f(-x)=-f(x),∴当x<0时,∴-1<f(x)<0.
因此值域为(-1,1),正确.
乙:当x≥0时,f(x)=
,f′(x)=
>0,∴函数f(x)单调递增,f(x)≥0;同理,当x<0时,函数f(x)单调递增,且f(x)<0.
∴若x1≠x2,则一定有f(x1)≠f(x2),正确;
丙:∵函数f(x)是奇函数,因此只考虑0<x即可.
f1(x)=f(x)=
,因此当n=1时成立.当n=2时,f2(x)=f(f1(x))=
=
=
也成立.
假设当n=k时成立,fk(x)≥
.
则当n=k+1时,fk+1(x)=f(fk(x))=
≥
=
,也成立.因此正确.
综上可得:甲乙丙都正确.
故选:D.
| x |
| 1+|x| |
| x |
| 1+x |
因此值域为(-1,1),正确.
乙:当x≥0时,f(x)=
| x |
| 1+x |
| 1 |
| (1+x)2 |
∴若x1≠x2,则一定有f(x1)≠f(x2),正确;
丙:∵函数f(x)是奇函数,因此只考虑0<x即可.
f1(x)=f(x)=
| x |
| 1+x |
| f1(x) |
| 1+f1(x) |
| ||
1+
|
| x |
| 1+2x |
假设当n=k时成立,fk(x)≥
| x |
| 1+kx |
则当n=k+1时,fk+1(x)=f(fk(x))=
| fk(x) |
| 1+fk(x) |
| ||
1+
|
| x |
| 1+(k+1)x |
综上可得:甲乙丙都正确.
故选:D.
点评:本题考查了函数的奇偶性单调性、数学归纳法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知a>0,b>0,3是3a与32b等比中项,
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、4 | ||||
B、3+2
| ||||
C、
| ||||
| D、2 |
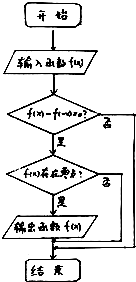 执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )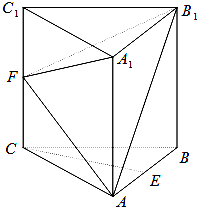 如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.
如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.