题目内容
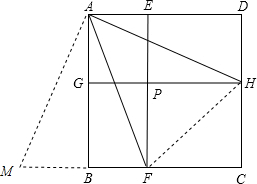
正方形ABCD被两垂直线段EF，GH分割为四个小矩形，P是EF和GH的交点．若矩形PFCH的面积恰是矩形AGPE面积的2倍，则∠HAF的大小是 ．
考点：进行简单的演绎推理
专题：立体几何
分析：作出辅助线BM，AM，FH，把求∠HAF的大小转化为求其全等三角形的对应角∠MAF的底数．
解答：
解：如图，连结FH，延长CB到M，使BM=DH，连结AM，
∵Rt△ABM≌Rt△ADH，
∴AM=AH，∠MAB=∠HAD，
∴∠MAH=∠MAB+∠BAH=∠BAH+∠HAD=90°，
设正方形的边长为a，AG=m，GP=n，则FC=a-n，CH=a-m，
由矩形PFCH的面积恰是矩形AGPE面积的2倍得：a2-（m+n）a+mn=2mn，
在Rt△FCH中，FH2=（a-n）2+（a-m）2，
∴FH2=FM2=（m+n）2，即FH=MF，
∵AF=AF，AH=AM，
∴△AMF≌△AHF，
∴∠MAF=∠HAF=45°，
故答案为：45°
∵Rt△ABM≌Rt△ADH，
∴AM=AH，∠MAB=∠HAD，
∴∠MAH=∠MAB+∠BAH=∠BAH+∠HAD=90°，
设正方形的边长为a，AG=m，GP=n，则FC=a-n，CH=a-m，
由矩形PFCH的面积恰是矩形AGPE面积的2倍得：a2-（m+n）a+mn=2mn，
在Rt△FCH中，FH2=（a-n）2+（a-m）2，
∴FH2=FM2=（m+n）2，即FH=MF，
∵AF=AF，AH=AM，
∴△AMF≌△AHF，
∴∠MAF=∠HAF=45°，
故答案为：45°
点评：本题考查的知识点是全等三角形的证明，考查了正方形对边平行且各内角均为直角的性质，构造△DAH的全等三角形△BAM并进行证明，是解答的关键．
练习册系列答案
相关题目
如图，在圆O中，已知弦AB=4，弦AC=6，那么| AO |
| BC |
| A、10 | ||
B、2
| ||
C、
| ||
| D、-10 |