题目内容
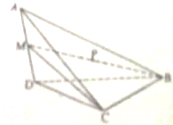 如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2| 2 |
(1)若∠BDC=45°,求直线CD与平面ACB所成角的大小;
(2)若二面角C-BM-D的大小为60°,求BC的长;
(3)若CD=x,对任意x∈[1.
| 2 |
考点:二面角的平面角及求法,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)过点D作DQ⊥AC于Q,则BC⊥AD,BC⊥DQ,从而DQ⊥平面ABC,直线CD与平面ABC所成角为∠DCA,由此能求出直线CD与平面ABC所成角.
(2)过C作CG⊥BD于G,过G作GN⊥BM于N,连结CN,则∠CNG是二面角C-BM-D的平面角,由此能推导出BC的长.
(3)过点D作DH⊥MC于H,连结BH,使BH∩PC=K,作KE∥DH,连结BH,使BH∩PC=K,作KE∥DH,且KE∩BD=E,由已知得点E为所求点,由此能求出y关于x的函数表达式,并求出y的最大值.
(2)过C作CG⊥BD于G,过G作GN⊥BM于N,连结CN,则∠CNG是二面角C-BM-D的平面角,由此能推导出BC的长.
(3)过点D作DH⊥MC于H,连结BH,使BH∩PC=K,作KE∥DH,连结BH,使BH∩PC=K,作KE∥DH,且KE∩BD=E,由已知得点E为所求点,由此能求出y关于x的函数表达式,并求出y的最大值.
解答:
解:(1)如图,过点D作DQ⊥AC于Q,
由AD⊥平面BCD,得BC⊥AD,
又BC⊥CD,AD∩CD=D,∴BC⊥DQ,
∵AC∩BC=C,∴DQ⊥平面ABC,
∴直线CD与平面ABC所成角为∠DCA,
在Rt△BCD中,∵∠BDC=45°,∴CD=BC=2,
在Rt△ACD中,∵AD=2,CD=2,∴∠DCA=45°,
∴直线CD与平面ABC所成角为45°.
(2)如图,由已知,平面ADB⊥平面BDC,
过C作CG⊥BD于G,∴CG⊥平面BMD,
过G作GN⊥BM于N,连结CN,
则∠CNG是二面角C-BM-D的平面角,
由已知得BM=
=3,设∠BDC=α,
则
=cosα,sinα=
=
,∴CD=2
cosα,
CG=2
cosαsinα,BC=2
sinα,
在Rt△BCG中,∠BCG=α,∴sinα=
,BG=2
sin2α,
在Rt△BNG中,由
=
,得NG=
,
在Rt△CNGk,∵tan∠CNG=tan60°=
=
=
,∴tanα=
,
∵α∈(0°,90°),∴α=60°,∴∠BDC=60°,
∴BC=BDsin∠BDC=2
sin60°=
.
(3)如图,过点D作DH⊥MC于H,连结BH,
使BH∩PC=K,
在平面HBD中,作KE∥DH,连结BH,使BH∩PC=K,
在平面HBD中,作KE∥DH,且KE∩BD=E,
下面证明点E为所求点,
∵BC⊥平面ADC,且BC?平面CMB,
∴平面CMB⊥平面ADC,
又∵DH⊥MC,∴DH⊥平面CMB,
∵EK∥DH,∴EK⊥平面CMB,∴平面CPE⊥平面CMB,
如图,在Rt△MDC中,
=
•
=
•
=
,
在Rt△MCB中
=
•
=1,
如图,通过补直角三角形为矩形,
利用相似三角形的性质,得
=
,
如图,在Rt△DHB中,由题意知△BEK∽△BDH,
∴
=
=
=
,
∴y=BE=
,x∈[1,
],
令μ=x2∈[1,2],则y=
=
=
+
,μ∈[1,2],
∵f(μ)=
+
在∈[1,2]上单调递减,
∴当μ=1时,ymax=
.

由AD⊥平面BCD,得BC⊥AD,
又BC⊥CD,AD∩CD=D,∴BC⊥DQ,
∵AC∩BC=C,∴DQ⊥平面ABC,
∴直线CD与平面ABC所成角为∠DCA,
在Rt△BCD中,∵∠BDC=45°,∴CD=BC=2,
在Rt△ACD中,∵AD=2,CD=2,∴∠DCA=45°,

∴直线CD与平面ABC所成角为45°.
(2)如图,由已知,平面ADB⊥平面BDC,
过C作CG⊥BD于G,∴CG⊥平面BMD,
过G作GN⊥BM于N,连结CN,
则∠CNG是二面角C-BM-D的平面角,
由已知得BM=
| 8+1 |
则
| CD |
| BD |
| CG |
| CD |
| CB |
| BD |
| 2 |

CG=2
| 2 |
| 2 |
在Rt△BCG中,∠BCG=α,∴sinα=
| BG |
| BC |
| 2 |
在Rt△BNG中,由
| NG | ||
2
|
| 1 |
| 3 |
2
| ||
| 3 |
在Rt△CNGk,∵tan∠CNG=tan60°=
| 3 |
| CG |
| NG |
2
| ||||
|
| 3 |
∵α∈(0°,90°),∴α=60°,∴∠BDC=60°,
∴BC=BDsin∠BDC=2
| 2 |
| 6 |

(3)如图,过点D作DH⊥MC于H,连结BH,
使BH∩PC=K,
在平面HBD中,作KE∥DH,连结BH,使BH∩PC=K,
在平面HBD中,作KE∥DH,且KE∩BD=E,
下面证明点E为所求点,
∵BC⊥平面ADC,且BC?平面CMB,
∴平面CMB⊥平面ADC,
又∵DH⊥MC,∴DH⊥平面CMB,
∵EK∥DH,∴EK⊥平面CMB,∴平面CPE⊥平面CMB,
如图,在Rt△MDC中,
| MH |
| HC |
| MH |
| DH |
| DH |
| HC |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
在Rt△MCB中
| MH |
| HC |
| 1 |
| x2 |
| MP |
| PB |
如图,通过补直角三角形为矩形,
利用相似三角形的性质,得
| HK |
| KB |
| x2 |
| 1+x2 |
如图,在Rt△DHB中,由题意知△BEK∽△BDH,
∴
| BE |
| BD |
| BK |
| BH |
| KB |
| HK+KB |
| x2+1 |
| 2x2+1 |
∴y=BE=
2
| ||
| 2x2+1 |
| 2 |
令μ=x2∈[1,2],则y=
2
| ||
| 2μ+1 |
2
| ||||||
| 2μ+1 |
=
| 2 |
| ||
| 2μ |
∵f(μ)=
| 2 |
| ||
| 2μ+1 |
∴当μ=1时,ymax=
4
| ||
| 3 |
点评:本题考查空间点、线、面位置关系,二面角等基础知识,考查空间思维能力、空间想象能力和运算求解能力.

练习册系列答案
相关题目
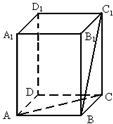 在正四棱柱ABCD-A1B1C1D1中,BC1与平面ABCD所成的角为60°,则BC1与AC所成的角为
在正四棱柱ABCD-A1B1C1D1中,BC1与平面ABCD所成的角为60°,则BC1与AC所成的角为