题目内容
已知函数y=f（x+1）的定义域为[-1，1]，则y=f（x）的定义域 ．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：由函数y=f（x+1）的定义域为[-1，1]得到x的范围是[-1，1]，由此求得x+1的范围得答案．
解答：
解：∵y=f（x+1）的定义域为[-1，1]，即-1≤x≤1，
得0≤x+1≤2．
∴y=f（x）的定义域是[0，2]．
故答案为：[0，2]．
得0≤x+1≤2．
∴y=f（x）的定义域是[0，2]．
故答案为：[0，2]．
点评：本题考查了函数的定义域及其求法，关键是掌握该类问题的解决方法，是基础题．
练习册系列答案
天天向上一本好卷系列答案
相关题目
设a=（
）
，b=（
）
，c=log
，则a，b，c的大小关系是（ ）
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| A、a＞c＞b |
| B、c＞a＞b |
| C、a＞b＞c |
| D、b＞a＞c |
已知函数f（x），x∈R，且在x=1处，f（x）存在极小值，则（ ）
| A、当x∈（-∞，1）时，f′（x）＞0；当x∈（1，+∞）时，f′（x）＜0 |
| B、当x∈（-∞，1）时，f′（x）＞0；当x∈（1，+∞）时，f′（x）＞0 |
| C、当x∈（-∞，1）时，f′（x）＜0；当x∈（1，+∞）时，f′（x）＞0 |
| D、当x∈（-∞，1）时，f′（x）＜0；当x∈（1，+∞）时，f′（x）＜0 |
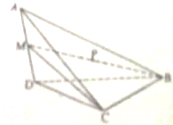如图，在四面体ABCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
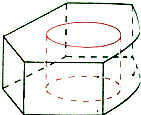有一堆规格相同的铁制（铁的密度是7.8/cm3）六角螺帽（如图）共重5.8kg，已知底面是正六边形，边长为12mm，内孔直径为10mm，高为10mm，问这堆螺帽大约有多少个（π取3.14，可用计算器）？