题目内容
集合M={m|m=a+b
，a∈Q，b∈Q}，若x∈M那么x2与集合M的关系是x2 M．
| 2 |
考点：元素与集合关系的判断
专题：集合
分析：根据元素和集合之间关系，判断即可
解答：
解：∵M={m|m=a+b
，a∈Q，b∈Q}，x∈M，
∴x2=（a+b
）2=a2+2b2+2
ab，
∴x∈M；
故答案为：∈
| 2 |
∴x2=（a+b
| 2 |
| 2 |
∴x∈M；
故答案为：∈
点评：本题考查元素与集合关系的判断，本题解题的关键是整理数字成集合中元素所对应的形式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知数列{an}的前n项和Sn=n2+
n，则a32-a22=（ ）
| 1 |
| 2 |
| A、9 | ||
| B、18 | ||
| C、21 | ||
D、
|
全集U={1，-2，3，-4，5，-6}，M={1，-2，3，-4}，则∁UM（ ）
| A、{1，3} |
| B、{5，-6} |
| C、{1，5} |
| D、{-4，5} |
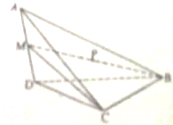如图，在四面体ABCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2