题目内容
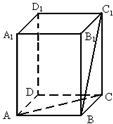 在正四棱柱ABCD-A1B1C1D1中,BC1与平面ABCD所成的角为60°,则BC1与AC所成的角为
在正四棱柱ABCD-A1B1C1D1中,BC1与平面ABCD所成的角为60°,则BC1与AC所成的角为考点:异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
分析:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.由于CC1⊥平面ABCD,则∠C1BC=60°,设正四棱柱ABCD-A1B1C1D1中的底面边长为a,侧棱长为b,即b=
a,再由余弦定理,即可得到.
| 3 |
解答:
 解:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.
解:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.
设正四棱柱ABCD-A1B1C1D1中的底面边长为a,侧棱长为b,
则由于CC1⊥平面ABCD,则∠C1BC=60°,
即有tan60°=
,即b=
a,
在△BA1C1中,BC1=BA1=
=2a,A1C1=
a,
cos∠BC1A1=
=
.
则BC1与AC所成的角为arccos
.
故答案为:arccos
.
 解:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.
解:连接A1C1,A1B,则AC∥A1C1,∠BC1A1即为BC1与AC所成的角.设正四棱柱ABCD-A1B1C1D1中的底面边长为a,侧棱长为b,
则由于CC1⊥平面ABCD,则∠C1BC=60°,
即有tan60°=
| b |
| a |
| 3 |
在△BA1C1中,BC1=BA1=
| a2+b2 |
| 2 |
cos∠BC1A1=
| 4a2+2a2-4a2 | ||
2×2a•
|
| ||
| 4 |
则BC1与AC所成的角为arccos
| ||
| 4 |
故答案为:arccos
| ||
| 4 |
点评:本题考查空间的直线和平面所成的角,异面直线所成的角的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知双曲线x2-2y2=2的左、右两焦点为F1,F2,动点P满足|PF1|+|PF2|=4,
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)若线段AB是曲线W的长为2的动弦,O为坐标原点,求△AOB面积的最大值.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)若线段AB是曲线W的长为2的动弦,O为坐标原点,求△AOB面积的最大值.
已知双曲线C:4x2-my2=4m(m>0)的一条渐近线方程为2x-3y=0,则双曲线C的焦距为( )
A、2
| ||
| B、6 | ||
C、2
| ||
| D、4m |
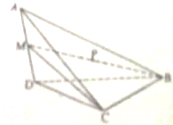 如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2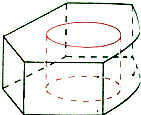 有一堆规格相同的铁制(铁的密度是7.8/cm3)六角螺帽(如图)共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?
有一堆规格相同的铁制(铁的密度是7.8/cm3)六角螺帽(如图)共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?