题目内容
19.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间大于10分钟的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{9}{10}$ |
分析 由电台整点报时的时刻是任意的知这是一个几何概型,电台整点报时知事件总数包含的时间长度是60,而他等待的时间大于10分钟的事件包含的时间长度是50,代入数据,得到结果
解答 解:由题意知这是一个几何概型,
∵电台整点报时,
∴事件总数包含的时间长度是60,
∵满足他等待的时间大于10分钟的事件包含的时间长度是50,
由几何概型公式得到P=$\frac{50}{60}=\frac{5}{6}$,
故选:B.
点评 本题考查了几何概型的概率求法;一般的,先要判断该概率模型,如果是几何概型,它的结果要通过长度、面积或体积之比来得到.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.设等差数列{an}的前n项和为Sn,若a4,a6是方程x2-18x+p=0的两根,那么S9=( )
| A. | 9 | B. | 81 | C. | 5 | D. | 45 |
4.已知点P在双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$上,点A满足$\overrightarrow{PA}=(t-1)\overrightarrow{OP}$(t∈R),且$\overrightarrow{OA}•\overrightarrow{OP}=64$,$\overrightarrow{OB}=(0,1)$,则$|{\overrightarrow{OB}•\overrightarrow{OA}}|$的最大值为( )
| A. | $\frac{5}{4}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{24}$ |
11.定义在R上的奇函数f(x)满足f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=3x-1,则f(9)=( )
| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
5.设随机变量X的分布列为P(X=k)=$\frac{k}{25}$,k=1,2,3,4,5,则P($\frac{1}{2}$<X<$\frac{5}{2}$)等于( )
| A. | $\frac{2}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{15}$ |
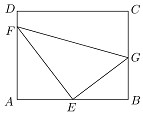 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.