题目内容
已知复数z=（a2-4）+（a+2）i（a∈R）
（Ⅰ）若z为纯虚数，求实数a的值；
（Ⅱ）若z在复平面上对应的点在直线x+2y+1=0上，求实数a的值．
（Ⅰ）若z为纯虚数，求实数a的值；
（Ⅱ）若z在复平面上对应的点在直线x+2y+1=0上，求实数a的值．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：（Ⅰ）若z为纯虚数，实部为0，虚部不为0，求实数a的值；
（Ⅱ）求出z在复平面上对应的点的坐标，代入直线x+2y+1=0，求实数a的值．
（Ⅱ）求出z在复平面上对应的点的坐标，代入直线x+2y+1=0，求实数a的值．
解答：
解：（Ⅰ）若z为纯虚数，则a2-4=0，且a+2≠0，解得实数a的值为2；
（Ⅱ）z在复平面上对应的点（a2-4，a+2），
在直线x+2y+1=0上，则a2-4+2（a+2）+1=0，
解得a=-1．
（Ⅱ）z在复平面上对应的点（a2-4，a+2），
在直线x+2y+1=0上，则a2-4+2（a+2）+1=0，
解得a=-1．
点评：本题考查复数的基本概念以及复数的几何意义，属于基础题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图，设AB，CD为⊙O的两直径，过B作PB垂直于AB，并与CD延长线相交于点P，过P作直线与⊙O分别交于E，F两点，连接AE，AF结分别与CD交于G，H．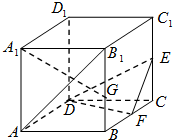
如图，已知正方体AC1棱长为2，E、F、G分别是CC1、BC和CD的中点．