题目内容
如图，设AB，CD为⊙O的两直径，过B作PB垂直于AB，并与CD延长线相交于点P，过P作直线与⊙O分别交于E，F两点，连接AE，AF结分别与CD交于G，H．（Ⅰ）设EF中点为C1，求证：O，C1，B，P四点共圆；
（Ⅱ）求证：OG=OH．
考点：与圆有关的比例线段,圆內接多边形的性质与判定
专题：直线与圆,立体几何
分析：（1）由已知条件推导出∠OC1P=∠PBO=90°，由此证明O，P，C1，B四点共圆
（2）利用对角互补得到四点共圆，利用相似得到边长相等．
（2）利用对角互补得到四点共圆，利用相似得到边长相等．
解答：
证明：（Ⅰ）∵过B作PB垂直于AB，并与CD延长线相交于点P，
过P作直线与⊙O分别交于E，F两点，EF中点为C1，
∴∠OC1P=∠PBO=90°，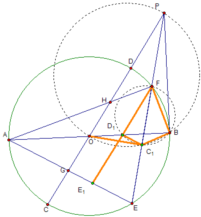
∴O，P，C1，B四点共圆．…（3分）
（Ⅱ）由（Ⅰ）∠OPC1=∠OBC1，
过F作FE1∥CD交AE于E1，交AB于D1，
连接D1C1，BC1，BF，
由D1F∥DC，知∠OPC1=∠D1FC1，
∴∠OBC1=∠D1FC1．
∴B，F，C1，D1，四点共圆．…（6分）
∴∠FBA=∠FC1D1=∠FEA，由此D1C1∥AE，…（8分）
∵C1是FE的中点，D1是FE1的中点，
∴
=
=
，∴OG=OH．…（10分）
过P作直线与⊙O分别交于E，F两点，EF中点为C1，
∴∠OC1P=∠PBO=90°，
∴O，P，C1，B四点共圆．…（3分）
（Ⅱ）由（Ⅰ）∠OPC1=∠OBC1，
过F作FE1∥CD交AE于E1，交AB于D1，
连接D1C1，BC1，BF，
由D1F∥DC，知∠OPC1=∠D1FC1，
∴∠OBC1=∠D1FC1．
∴B，F，C1，D1，四点共圆．…（6分）
∴∠FBA=∠FC1D1=∠FEA，由此D1C1∥AE，…（8分）
∵C1是FE的中点，D1是FE1的中点，
∴
| OG |
| D1E1 |
| AO |
| AD1 |
| OH |
| D1F |
点评：本题考查四点共圆的证明，考查线段长相等的证明，是中档题，解题时要认真审题，注意四圆共圆的性质的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目