题目内容
已知二项式(5x-
)n展开式中各项系数之和是各项二项式系数之和的16倍;
(1)求n;
(2)求展开式中二项式系数最大的项;
(3)求展开式中所有x的有理项.
| 1 | ||
|
(1)求n;
(2)求展开式中二项式系数最大的项;
(3)求展开式中所有x的有理项.
考点:二项式系数的性质,二项式定理的应用
专题:二项式定理
分析:(1)由已知得:4n=16•2n,即 22n=2n+4,由此求得 n的值.
(2)根据n=4,可得展开式中二项式系数最大的项为第三项,从而根据通项公式求得第三项.
(3)在通项公式中,令x的幂指数4-
r取整数,求得r的值,可得展开式中所有的有理项.
(2)根据n=4,可得展开式中二项式系数最大的项为第三项,从而根据通项公式求得第三项.
(3)在通项公式中,令x的幂指数4-
| 3 |
| 2 |
解答:
解:(1)由已知得:4n=16•2n,即 22n=2n+4,∴2n=n+4,∴n=4.
(2)根据n=4,可得展开式中二项式系数最大的项为第三项,
即T3=(-1)2
52x=150x.
(3)根据通项公式为 Tr+1=
•54-r•(-1)r•x4-
r,
令4-
r∈z,可得 r=0、2、4,
所以展开式中所有f(x)的有理项为:T1=625x4,T3=150x,T5=x-2.
(2)根据n=4,可得展开式中二项式系数最大的项为第三项,
即T3=(-1)2
| C | 2 4 |
(3)根据通项公式为 Tr+1=
| C | r 4 |
| 3 |
| 2 |
令4-
| 3 |
| 2 |
所以展开式中所有f(x)的有理项为:T1=625x4,T3=150x,T5=x-2.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
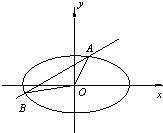 直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点).
直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点).