题目内容
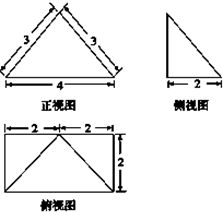 已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中的最大面积是( )
已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中的最大面积是( )| A、6 | ||
| B、8 | ||
C、2
| ||
| D、3 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个以俯视图为底面的四棱锥,分别计算出四个侧面的侧面积,可得答案.
解答:
解:因为三视图复原的几何体是四棱锥,顶点在底面的射影是底面矩形的长边的中点,底面边长分别为4,2,
后面是等腰三角形,腰为3,所以后面的三角形的高为:
=
,
所以后面三角形的面积为:
×4×
=2
.
两个侧面面积为:
×2×3=3,
前面三角形的面积为:
×4×
=6,
四棱锥P-ABCD的四个侧面中面积最大的是前面三角形的面积:6.
故选:A.
后面是等腰三角形,腰为3,所以后面的三角形的高为:
| 32-22 |
| 5 |
所以后面三角形的面积为:
| 1 |
| 2 |
| 5 |
| 5 |
两个侧面面积为:
| 1 |
| 2 |
前面三角形的面积为:
| 1 |
| 2 |
|
四棱锥P-ABCD的四个侧面中面积最大的是前面三角形的面积:6.
故选:A.
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
 如图所示直三棱柱ABG-DCE中ABCD是边长为2的正方形,DE⊥平面ABCD,F为AG的中点,BE与平面ABCD所成角的正切值为
如图所示直三棱柱ABG-DCE中ABCD是边长为2的正方形,DE⊥平面ABCD,F为AG的中点,BE与平面ABCD所成角的正切值为
| ||
| 2 |
(1)求证:AC∥平面EFB;
(2)求二面角F-BE-A的大小.
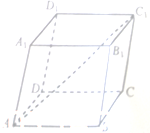
在平行六面体ABCD-A1B1C1D1中,
=x
+2y
+3z
,则x+y+z=( )
| AC1 |
| AB |
| AD |
| AA1 |

A、
| ||
B、
| ||
C、
| ||
D、
|
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若E为线段PF的中点,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、100 cm3 |
| B、108 cm3 |
| C、84 cm3 |
| D、92 cm3 |
对一切实数x,不等式ax2-ax-2<0恒成立,则实数a的取值范围是( )
| A、[-8,0] |
| B、(-8,0) |
| C、(-8,0] |
| D、[0,8) |
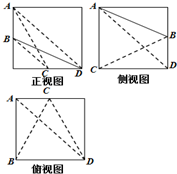 在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )
在棱长为2的正方体内有一四面体A-BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A-BCD的体积为( )