题目内容
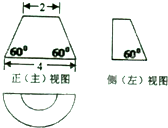
已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
| A、100 cm3 |
| B、108 cm3 |
| C、84 cm3 |
| D、92 cm3 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：如图所示，原几何体为：一个长宽高分别为6，3，6的长方体砍去一个三棱锥，底面为直角边分别为3，4直角三角形，高为4．利用长方体与三棱锥的体积计算公式即可得出．
解答：
解：如图所示，原几何体为
：
一个长宽高分别为6，3，6的长方体砍去一个三棱锥，底面为直角边分别为3，4直角三角形，高为4．
因此该几何体的体积=3×6×6-
×
×3×4×4
=108-8
=100．
故选：A
：一个长宽高分别为6，3，6的长方体砍去一个三棱锥，底面为直角边分别为3，4直角三角形，高为4．
因此该几何体的体积=3×6×6-
| 1 |
| 3 |
| 1 |
| 2 |
=108-8
=100．
故选：A
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
如题图所示为某空间几何体的三视图，则该几何体的表面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直线的向量参数方程为（x，y，z）=（5，0，3）+t（0，3，0），当t=
时，则对应直线上的点的坐标是（ ）
| 1 |
| 2 |
| A、（5，0，3） | ||||
B、（
| ||||
C、（5，
| ||||
D、（
|
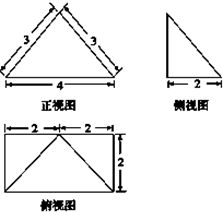已知四棱锥P-ABCD的三视图如图所示，则四棱锥P-ABCD的四个侧面中的最大面积是（ ）| A、6 | ||
| B、8 | ||
C、2
| ||
| D、3 |
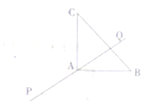如图，在Rt△ABC中，|