题目内容
对一切实数x，不等式ax2-ax-2＜0恒成立，则实数a的取值范围是（ ）
| A、[-8，0] |
| B、（-8，0） |
| C、（-8，0] |
| D、[0，8） |
考点：函数恒成立问题
专题：函数的性质及应用,不等式的解法及应用
分析：当a=0时对于任意实数x不等式显然成立；当a≠0时，由二次不等式对应的二次函数的图象开口向下且判别式小于0列不等式组求解a的范围．
解答：
解：当a=0时，不等式ax2-ax-2＜0化为-2＜0，此式显然成立；
当a≠0时，要使对一切实数x，不等式ax2-ax-2＜0恒成立，
则
，解得：-8＜a＜0．
综上，对一切实数x，不等式ax2-ax-2＜0恒成立的实数a的取值范围是（-8，0]．
故选：C．
当a≠0时，要使对一切实数x，不等式ax2-ax-2＜0恒成立，
则
|
综上，对一切实数x，不等式ax2-ax-2＜0恒成立的实数a的取值范围是（-8，0]．
故选：C．
点评：本题考查了恒成立问题，考查了分类讨论的数学思想方法，训练了由二次不等式成立求解参数的取值范围问题，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
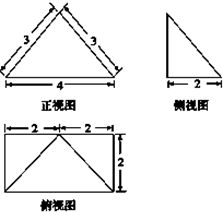已知四棱锥P-ABCD的三视图如图所示，则四棱锥P-ABCD的四个侧面中的最大面积是（ ）| A、6 | ||
| B、8 | ||
C、2
| ||
| D、3 |
已知某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
圆O的半径为1，P为圆周上一点，现将如图放置的边长为1的正方形（实线所示，正方形的顶点A与点P重合）沿圆周逆时针滚动，点A第一次回到点P的位置，则点A走过的路径的长度为