题目内容
设函数f(x)=lnx+
,m∈R.
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数g(x)=f′(x)-
零点的个数.
| m |
| x |
(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;
(Ⅱ)讨论函数g(x)=f′(x)-
| x |
| 3 |
考点:利用导数研究函数的极值
专题:计算题,分类讨论,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求出导数,令它大于0,得到增区间,令小于0,得到减区间,从而求出极小值;
(Ⅱ)求出g(x)的表达式,令它为0,则有m=-
x3+x.设h(x)=-
x3+x,其定义域为(0,+∞).则g(x)的零点个数为h(x)与y=m的交点个数,求出单调区间得到最值,画出h(x)的图象,由图象即可得到零点个数.
(Ⅱ)求出g(x)的表达式,令它为0,则有m=-
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:(Ⅰ)当m=e时,f(x)=lnx+
,其定义域为(0,+∞).
f′(x)=
-
=
令f′(x)=0,x=e.f′(x)>0,则0<x<e;f′(x)<0,则x>e.
故当x=e时,f(x)取得极小值f(e)=lne+
=2.
(Ⅱ)g(x)=f′(x)-
=
-
-
=
,其定义域为(0,+∞).
令g(x)=0,得m=-
x3+x.
设h(x)=-
x3+x,其定义域为(0,+∞).则g(x)的零点个数为h(x)与y=m的交点个数.
h′(x)=-x2+1=-(x+1)(x-1)
故当x=1时,h(x)取得最大值h(1)=
.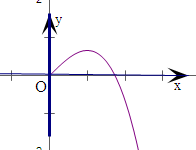
作出h(x)的图象,
由图象可得,
①当m>
时,g(x)无零点;
②当m=
或m≤0时,g(x)有且仅有1个零点;
③当0<m<
时,g(x)有两个零点.
| e |
| x |
f′(x)=
| 1 |
| x |
| e |
| x2 |
| x-e |
| x2 |
令f′(x)=0,x=e.f′(x)>0,则0<x<e;f′(x)<0,则x>e.
故当x=e时,f(x)取得极小值f(e)=lne+
| e |
| e |
(Ⅱ)g(x)=f′(x)-
| x |
| 3 |
| 1 |
| x |
| m |
| x2 |
| x |
| 3 |
| 3x-3m-x3 |
| 3x2 |
令g(x)=0,得m=-
| 1 |
| 3 |
设h(x)=-
| 1 |
| 3 |
h′(x)=-x2+1=-(x+1)(x-1)
| x | (0,1) | 1 | (1,+∞) |
| h′(x) | + | 0 | - |
| h(x) | 递增 | 极大值 | 递减 |
| 2 |
| 3 |

作出h(x)的图象,
由图象可得,
①当m>
| 2 |
| 3 |
②当m=
| 2 |
| 3 |
③当0<m<
| 2 |
| 3 |
点评:本题考查导数的综合运用:求单调区间和求极值,考查函数的零点问题,同时考查分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
