题目内容
设△ABC三条边的边长分别为a,b,c,对应的角分别为A,B,C
(1)设2b=a+c,且角B的取值集合为M,当x∈M时,求f(x)=sin(4x-
)的值域;
(2)设角B的平分线交边AC于D,且角B取(1)中的最大值(不含2b=a+c),
=2
,BD=4
,求其三边a,b,c的值.
(1)设2b=a+c,且角B的取值集合为M,当x∈M时,求f(x)=sin(4x-
| π |
| 6 |
(2)设角B的平分线交边AC于D,且角B取(1)中的最大值(不含2b=a+c),
| AD |
| DC |
| 3 |
考点:平面向量的综合题
专题:综合题,平面向量及应用
分析:(1)利用余弦定理,结合基本不等式求出B的范围,再求f(x)=sin(4x-
)的值域;
(2)由题意B=
,由角平分线的性质可得c=2a,由余弦定理求出AD,DC,建立方程,求出a,c,利用余弦定理求出b即可.
| π |
| 6 |
(2)由题意B=
| π |
| 3 |
解答:
解:(1)由题意,cosB=
=
(
+
)-
≥
,
∴0<B≤
,
x∈M时,-
<4x-
≤
,
∴-
≤sin(4x-
)≤1,
∴f(x)=sin(4x-
)的值域为[
,1];
(2)由题意B=
,由角平分线的性质可得c=2a,则AD=
,DC=
∵
=2
,
∴
=2
∴a=6,
∴c=12,
∴b=
=6
.
| a2+c2-b2 |
| 2ac |
| 3 |
| 8 |
| a |
| c |
| c |
| a |
| 1 |
| 4 |
| 1 |
| 2 |
∴0<B≤
| π |
| 3 |
x∈M时,-
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
∴f(x)=sin(4x-
| π |
| 6 |
| 1 |
| 2 |
(2)由题意B=
| π |
| 3 |
4a2+48-2×2a×4
|
a2+48-2×a×4
|
∵
| AD |
| DC |
∴
4a2+48-2×2a×4
|
a2+48-2×a×4
|
∴a=6,
∴c=12,
∴b=
62+122-2×6×12×
|
| 3 |
点评:本题考查余弦定理,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
一个几何体的三视图如图所示,那么该几何体的体积是( )
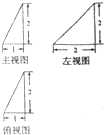

| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
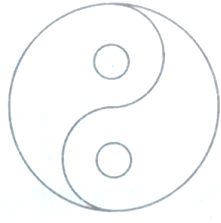 给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有
给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有