题目内容
16.方程式x2-2x-3=0的根是3或-1.分析 因式分解可得x2-2x-3=(x-3)(x+1),从而解得.
解答 解:因式分解可得,
x2-2x-3=(x-3)(x+1),
∴x2-2x-3=0可化为
(x-3)(x+1)=0,
∴x=3或x=-1;
故答案为:3或-1.
点评 本题考查了因式分解的应用及一元二次方程的解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某企业生产某种产品,在2011年至2015年所获利润(单位:十万元)的数据如下表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2011年至2015年该企业所获利润的变化情况,并预测该企业在2016年的所获利润.附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 利润y | 5.8 | 6.6 | 7.1 | 7.4 | 8.1 |
(Ⅱ)利用(Ⅰ)中的回归方程,分析2011年至2015年该企业所获利润的变化情况,并预测该企业在2016年的所获利润.附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
8.将函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的图象向右平移$\frac{π}{4}$个单位,得到函数g(x)的图象,函数g(x)的相邻的两个极值点的距离等于$\frac{π}{2}$,则g(x)的单调递减区间是( )
| A. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | B. | [kπ+$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z | ||
| C. | [2kπ+$\frac{5π}{12}$,2kπ+$\frac{11π}{12}$],k∈Z | D. | [2kπ-$\frac{π}{12}$,2kπ+$\frac{5π}{12}$],k∈Z |
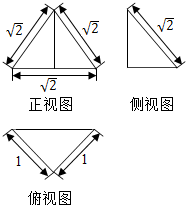 如图所示为一个几何体的三视图:
如图所示为一个几何体的三视图: