Question

1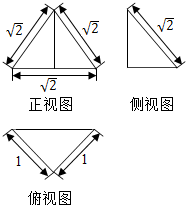．如图所示为一个几何体的三视图：
（1）指出该空间几何体的结构特征：
（2）求该几何体的外接球的表面积．

Answer 1

分析 （1）由三视图现状可知几何体为三棱锥，由俯视图可知底面为直角三角形，由侧视图可知侧面与底面垂直；
（2）作出直观图，由三棱锥的结构特征可知球心在棱锥的高上，列出方程解出半径．

解答 解：（1）该空间几何体为底面是等腰直角三角形的三棱锥，且过底面斜边的侧面与底面垂直．
（2）设该棱锥为S-ABC，外接球球心为O，如图，
∵AB=BC=1，AC=$\sqrt{2}$，∴AB⊥BC，∴AC为截面ABC的直径，
取AC中点D，连接SD，∵SA=SC=AC=$\sqrt{2}$，∴SD⊥AC．∴AD=$\frac{1}{2}AC=\frac{\sqrt{2}}{2}$，SD=$\sqrt{S{A}^{2}-A{D}^{2}}$=$\frac{\sqrt{6}}{2}$．
∵平面SAC⊥平面ABC，平面SAC∩平面ABC=AC，
∴SD⊥平面ABC，∴O在直线SD上．
设球O的半径为R，则OA=SO=R，OD=SD-SO=$\frac{\sqrt{6}}{2}-R$，
∵OA²=AD²+OD²，∴R²=（$\frac{\sqrt{2}}{2}$）²+（$\frac{\sqrt{6}}{2}-R$）²，
解得R=$\frac{\sqrt{6}}{3}$．
∴该几何体的外接球的表面积为4πR²=$\frac{8π}{3}$．

点评 本题考查了棱锥的结构特征，及外接球的有关计算，画出直观图解出外接球半径是关键．