题目内容
已知函数f(x)=
,x∈[2,4]对于满足2<x1<x2<4的任意x1,x2,给出下列结论:
①x1f(x2)>x2f(x1)
②x2f(x1)>x1f(x2)
③(x2-x1)[f(x2)-f(x1)]<0
④(x2-x1)[f(x2)-f(x1)]>0
其中正确的是( )
| 4-(x-2)2 |
①x1f(x2)>x2f(x1)
②x2f(x1)>x1f(x2)
③(x2-x1)[f(x2)-f(x1)]<0
④(x2-x1)[f(x2)-f(x1)]>0
其中正确的是( )
| A、①③ | B、①④ | C、②③ | D、②④ |
考点:函数单调性的性质
专题:函数的性质及应用
分析:易得函数f(x)=
在∈[2,4]上为减函数,故由减函数的性质得出结论.
| 4-(x-2)2 |
解答:
解:∵g(x)=4-(x-2)2在[2,4]上为减函数,
∴由复合函数的单调性法则可知f(x)=
在[2,4]上为减函数,
又∵2<x1<x2<4,
∴f(x2)<f(x1),∴x2f(x1)>x1f(x2) 故②正确;
又由x2-x1>0,f(x2)-f(x1)<0得 (x2-x1)[f(x2)-f(x1)]<0 故③正确.
故选C.
∴由复合函数的单调性法则可知f(x)=
| 4-(x-2)2 |
又∵2<x1<x2<4,
∴f(x2)<f(x1),∴x2f(x1)>x1f(x2) 故②正确;
又由x2-x1>0,f(x2)-f(x1)<0得 (x2-x1)[f(x2)-f(x1)]<0 故③正确.
故选C.
点评:利用减函数的性质以及不等式的有关性质很容易得出结论,属基础题.

练习册系列答案
相关题目
将
化为角度是( )
| 4π |
| 3 |
| A、480° | B、240° |
| C、120° | D、235° |
若函数f(x)=
f′(-1)x2-2x+3,则f′(-1)的值为( )
| 1 |
| 2 |
| A、0 | B、-1 | C、1 | D、2 |
若2x2-x-6<1,则( )
| A、x<-2或x>3 |
| B、-2<x<3 |
| C、x<-3或x>2 |
| D、-3<x<2 |
复数z=(m-1)(m-8)+
ilog2m(m∈R)是纯虚数,则
=( )
| 1 |
| 3 |
| 1 |
| 1-z |
| A、1+i | ||||
| B、1-i | ||||
C、
| ||||
D、
|
已知复数z满足
=i(其中i是虚数单位),则z为( )
| z+2 |
| z-2 |
| A、2i | B、-2i | C、i | D、-i |
C的方程为(x-1)2+(y-2)2=4,则圆C的圆心坐标和半径r分别为( )
| A、(1,2),r=2 |
| B、(-1,-2),r=2 |
| C、(1,2),r=4 |
| D、(-1,-2),r=4 |
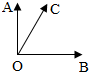 如图所示:|
如图所示:|| OA |
| OB |
| 3 |
| OA |
| OB |
| π |
| 6 |
| OC |
| OA |
| OB |
| λ |
| μ |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|