题目内容
1.设不等式组$\left\{\begin{array}{l}{x+2y-5≤0}\\{x≥-1}\\{y≥0}\end{array}\right.$,表示的平面区域为D,点A(3,0),原点O(0,0),在区域D内随机取一点M,则点M满足|MA|≥2|MO|的概率是( )| A. | $\frac{2π}{9}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{9}$ | D. | $\frac{π}{12}$ |
分析 求出M的轨迹,再利用面积为测度,即可求出概率.
解答  解:设M(x,y),则
解:设M(x,y),则
∵|MA|≥2|MO|,
∴(x-3)2+y2≥4x2+4y2,
∴(x+1)2+y2≤4,
如图所示,直角三角形的高为3,面积为$\frac{1}{2}×6×3$=9
圆落在三角形内的面积为$\frac{1}{4}π•4$=π,
∴点M满足|MA|≥2|MO|的概率是$\frac{π}{9}$.
故选:C.
点评 本题考查概率的计算,考查轨迹问题,正确求出M的轨迹是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
11.已知集合$A=\left\{{\left.x\right|{{log}_2}({x-1})≤1}\right\},B=\left\{{\left.x\right|{x^2}-x-6≤0}\right\}$,则A∩B=( )
| A. | {x|x≤3} | B. | {x|-2≤x≤3} | C. | {x|1<x≤3} | D. | {x|-2≤x<1} |
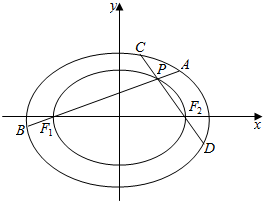 如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.
如图,已知点F1,F2是椭圆C1:$\frac{{x}^{2}}{2}$+y2=1的两个焦点,椭圆C2:$\frac{{x}^{2}}{2}$+y2=λ经过点F1,F2,点P是椭圆C2上异于F1,F2的任意一点,直线PF1和PF2与椭圆C1的交点分别是A,B和C,D,设AB、CD的斜率为k,k′.