题目内容
4.双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别是F1(-c,0),F2(c,0),M,N两点在双曲线上,且MN∥F1F2,|F1F2|=3|MN|,线段F1N交双曲线C于点Q,且Q是线段F1N的中点,则双曲线C的离心率为( )| A. | 3 | B. | $2\sqrt{2}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{5}+1}}{3}$ |
分析 由题意可设N($\frac{1}{3}$c,y),由中点坐标公式可得Q的坐标,将N,Q的坐标分别代入双曲线方程,解方程结合离心率公式,即可得到所求值.
解答 解:因为MN∥F1F2,|F1F2|=3|MN|,F1(-c,0),
所以|MN|=$\frac{2}{3}$c,则可设N($\frac{1}{3}$c,y),
由Q是线段F1N的中点知$Q(-\frac{c}{3},\frac{1}{2}y)$.
分别将N,Q的坐标代入双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,
得$\frac{{\frac{c^2}{9}}}{a^2}-\frac{y^2}{b^2}=1$,$\frac{\frac{{c}^{2}}{9}}{{a}^{2}}$-$\frac{{y}^{2}}{4{b}^{2}}$=1,解得$\frac{c^2}{a^2}=9$,
所以$e=\frac{c}{a}=3$.
故选:A.
点评 本题考查双曲线的方程和性质,注意运用中点坐标公式和点满足双曲线的方程,考查运算能力,属于中档题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
19.已知 $a={({\frac{1}{3}})^3},b={x^3},c=lnx$,当x>2时,a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
9.已知条件p:|x-4|≤6,条件q:x≤1+m,若p是q的充分不必要条件,则m的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,9] | C. | [1,9] | D. | [9,+∞) |
16.过球O表面上一点A引三条长度相等的弦AB、AC、AD,且两两夹角都为60°,若球半径为R,则弦AB的长度为( )
| A. | $\frac{{2\sqrt{6}}}{3}R$ | B. | $\frac{{\sqrt{6}}}{3}R$ | C. | R | D. | $\sqrt{6}R$ |
14.函数$f(x)=\sqrt{{2^x}-\frac{1}{4}}+ln({1-x})$的定义域是( )
| A. | [-1,2) | B. | (-2,1) | C. | (-2,1] | D. | [-2,1) |
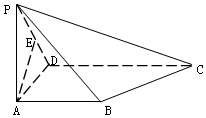 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.