题目内容
12.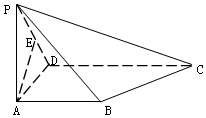 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.(1)求证:PA=AD;
(2)求点A到平面PBC的距离.
分析 (1)证明AE⊥平面PCD,AE⊥PD,利用E为PD中点P,可得A=AD;
(2)利用等体积方法,求点A到平面PBC的距离.
解答 (1)证明:∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,
∵CD⊥AD,PA∩AD=A,
∴CD⊥平面PAD,
∵AE?平面PAD,
∴AE⊥CD,
∵PC⊥AE,PC∩CD=C,
∴AE⊥平面PCD,
∵PD?平面PCD,
∴AE⊥PD,
∵E为PD中点,
∴PA=AD;
(2)解:由题意,PA=AD=1,S△ABC=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
△PBC中,PB=CB=$\sqrt{2}$,PC=$\sqrt{6}$,∴S△PBC=$\frac{1}{2}×\sqrt{6}×\sqrt{2-\frac{3}{2}}$=$\frac{\sqrt{3}}{2}$
设点A到平面PBC的距离为h,则$\frac{1}{3}×\frac{1}{2}×1=\frac{1}{3}×\frac{\sqrt{3}}{2}h$,∴h=$\frac{\sqrt{3}}{3}$.
点评 本题考查线面垂直的判定与性质,考查点到平面距离的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
20.过点(1,1)的抛物线y=ax2的焦点坐标为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({0,-\frac{1}{4}})$ | C. | $({0,\frac{1}{4}})$ | D. | $({\frac{1}{4},0})$ |
4.双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别是F1(-c,0),F2(c,0),M,N两点在双曲线上,且MN∥F1F2,|F1F2|=3|MN|,线段F1N交双曲线C于点Q,且Q是线段F1N的中点,则双曲线C的离心率为( )
| A. | 3 | B. | $2\sqrt{2}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{5}+1}}{3}$ |
1.已知(x,y)满足$\left\{\begin{array}{l}y≥x\\ y≤2\\ y≥2-x\end{array}$,z=x+ay,若z取得最大值的最优解有无数个,则a=( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 无法确定 |
2.设${y_1}={4^{0.2}},{y_2}={({\frac{1}{2}})^{-0.3}},{y_3}={log_{\frac{1}{2}}}8$,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y2>y1>y3 | C. | y1>y2>y3 | D. | y1>y3>y2 |
 已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,l与直线m:x+3y+6=0相交于N.
已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,l与直线m:x+3y+6=0相交于N.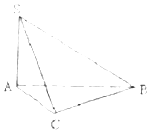 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3},SB=2\sqrt{2}$.
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3},SB=2\sqrt{2}$.