题目内容
19.已知 $a={({\frac{1}{3}})^3},b={x^3},c=lnx$,当x>2时,a,b,c的大小关系为( )| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
分析 利用函数的单调性即可得出.
解答 解:$a=(\frac{1}{3})^{3}$<1,取x=e时,b=e3>1,c=lne=1.
所以a<c<b.
故选:B.
点评 本题考查了函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10.把函数y=sin(2x+$\frac{π}{6}$)图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再将图象向右平移$\frac{π}{3}$个单位,得到函数y=g(x),那么g($\frac{π}{3}$)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
4.双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别是F1(-c,0),F2(c,0),M,N两点在双曲线上,且MN∥F1F2,|F1F2|=3|MN|,线段F1N交双曲线C于点Q,且Q是线段F1N的中点,则双曲线C的离心率为( )
| A. | 3 | B. | $2\sqrt{2}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{5}+1}}{3}$ |
11.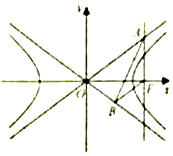 如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
 如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
9.如果圆(x-a)2+(y-a)2=8上总存在两个点到原点的距离为$\sqrt{2}$,则实数a的取值范围是( )
| A. | (-3,3) | B. | (-1,1) | C. | (-3,1) | D. | (-3,-1)∪(1,3) |
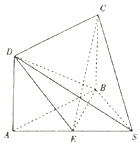 如图,在四棱锥S-ABCD中,四边形为ABCD矩形,E为SA的中点,SA=SB,AB=2$\sqrt{3}$,BC=3.
如图,在四棱锥S-ABCD中,四边形为ABCD矩形,E为SA的中点,SA=SB,AB=2$\sqrt{3}$,BC=3.