题目内容
14.已知函数f(x)=xm-$\frac{2}{x}$且f(4)=$\frac{7}{2}$,(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并用定义证明.
(3)求f(x)在[2,5]上的值域.
分析 (1)根据$f(4)=\frac{7}{2}$,带入计算可得m的值.
(2)求解f(x)的解析式,利用定义域证明即可.
(3)利用单调性求解f(x)在[2,5]上的值域即可.
解答 解:(1)∵函数f(x)=xm-$\frac{2}{x}$,
由f(4)=$\frac{7}{2}$,
可得:${4}^{m}-\frac{1}{2}=\frac{7}{2}$,
解得:m=1.
∴m的值为1.
(2)由(1)可得f(x)=x-$\frac{2}{x}$,
设0<x1<x2,则$f({x}_{1})-f({x}_{2})={x}_{1}-{x}_{2}-\frac{2}{{x}_{1}}+\frac{2}{{x}_{2}}$=${(x}_{1}-{x}_{2})-\frac{2({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}$<0,
即f(x1)<f(x2),
∴f(x)在(0,+∞)上是单调增函数.
(3)由2可知f(x)在(0,+∞)上是单调增函数,即在[2,5]上的也是增函数.
当x=2时,f(x)取得最小值为1,
当x=5时,f(x)取得最大值为$\frac{23}{5}$,
故得f(x)在[2,5]上的值域为[1,$\frac{23}{5}$].
点评 本题主要考擦了函数解析式的求法,单调性的定义证明以及利用单调性求解值域问题.属于基础题

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,点B是虚轴上的一个顶点,线段BF与双曲线C的右支交于点A,若$\overrightarrow{BA}$=2$\overrightarrow{AF}$,且|$\overrightarrow{BF}$|=4,则双曲线C的方程为( )
| A. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{6}$=1 |
6.已知抛物线y2=4x的焦点F,若A,B是该抛物线上的点,∠AFB=90°,线段AB中点M在抛物线的准线上的射影为N,则$\frac{|MN|}{|AB|}$的最大值为 ( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
4.双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别是F1(-c,0),F2(c,0),M,N两点在双曲线上,且MN∥F1F2,|F1F2|=3|MN|,线段F1N交双曲线C于点Q,且Q是线段F1N的中点,则双曲线C的离心率为( )
| A. | 3 | B. | $2\sqrt{2}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{5}+1}}{3}$ |
 已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,l与直线m:x+3y+6=0相交于N.
已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,l与直线m:x+3y+6=0相交于N.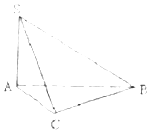 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3},SB=2\sqrt{2}$.
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3},SB=2\sqrt{2}$.