题目内容
14.函数$f(x)=\sqrt{{2^x}-\frac{1}{4}}+ln({1-x})$的定义域是( )| A. | [-1,2) | B. | (-2,1) | C. | (-2,1] | D. | [-2,1) |
分析 根据函数f(x)的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:函数$f(x)=\sqrt{{2^x}-\frac{1}{4}}+ln({1-x})$,
∴$\left\{\begin{array}{l}{{2}^{x}-\frac{1}{4}≥0}\\{1-x>0}\end{array}\right.$,
解得-2≤x<1,
∴f(x)的定义域是[-2,1).
故选:D.
点评 本题考查了根据函数解析式求定义域的应用问题,关键是列出使解析式有意义的不等式组.

练习册系列答案
相关题目
4.双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点分别是F1(-c,0),F2(c,0),M,N两点在双曲线上,且MN∥F1F2,|F1F2|=3|MN|,线段F1N交双曲线C于点Q,且Q是线段F1N的中点,则双曲线C的离心率为( )
| A. | 3 | B. | $2\sqrt{2}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{5}+1}}{3}$ |
5.已知抛物线C:y2=4x的焦点为F,准线为l,若射线y=2(x-1)(x≤1)与C,l分别交于P、Q两点,则$\frac{|PQ|}{|PF|}$=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |
2.设${y_1}={4^{0.2}},{y_2}={({\frac{1}{2}})^{-0.3}},{y_3}={log_{\frac{1}{2}}}8$,则y1,y2,y3的大小关系是( )
| A. | y3>y1>y2 | B. | y2>y1>y3 | C. | y1>y2>y3 | D. | y1>y3>y2 |
9.如果圆(x-a)2+(y-a)2=8上总存在两个点到原点的距离为$\sqrt{2}$,则实数a的取值范围是( )
| A. | (-3,3) | B. | (-1,1) | C. | (-3,1) | D. | (-3,-1)∪(1,3) |
19.已知集合M={x|-1≤x<8},N={x|x>4},则M∪N=( )
| A. | (4,+∞) | B. | [-1,4) | C. | (4,8) | D. | [-1,+∞) |
6.一个正三棱柱(底面为正三角形的直棱柱)的三视图如图所示,则这个正三棱柱的体积为( )
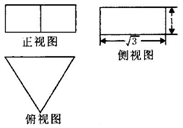

| A. | $6\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |