Question

12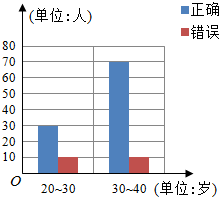．“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（I）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关；说明你的理由；（下面的临界值表供参考）

P（K2≥k0）	0.10	0.05	0.010	0.005
k0	2.706	3.841	6.635	7.879

（2）现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手，并从这6名选手中抽取2名幸运选手，求2名幸运选手中至少有一人在20～30岁之间的概率．
（参考公式：K²=$\frac{n（ad-bc）^{2}}{（a+b）（a+c）（c+d）（d+b）}$．其中n=a+b+c+d）

Answer 1

分析 （1）根据所给的二维条形图得到列联表，利用公式求出k²=3＞2.706，即可得出结论；
（2）按照分层抽样方法可知：20～30（岁）抽取：6×$\frac{40}{120}$=2（人）；30～40（岁）抽取：6×$\frac{80}{120}$=4（人），在上述抽取的6名选手中，年龄在20～30（岁）有2人，年龄在30～40（岁）有4人，利用列举法求出基本事件数，即可求出至少有一人年龄在20～30岁之间的概率．

解答 解：（1）2×2列联表：

年 龄 正误	正确	错误	合计
20～30	10	30	40
30～40	10	70	80
合计	20	100	120

---（6分）
则${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（a+c）（c+d）（d+b）}=\frac{{120×{{（10×70-10×30）}^2}}}{20×40×80×100}=3＞2.706$
所以有90%的把握认为猜对歌曲名称与否和年龄有关．-----（8分）
（2）设事件A为2名幸运选手中至少有一人在20～30岁之间，由已知得20～30岁之间的人数为2人设为a，b，30～40岁之间的人数为4人设为c，d，e，f，从6人中取2人的结果如下共为有15种，
ab，ac，ad，ae，af，bc，bd，be，bf，cd，ce，cf，de，df，ef-----（10分）
事件A的包含如下结果：ab，ac，ad，ae，af，bc，bd，be，bf共有9种-----（11分）
则$P（A）=\frac{9}{15}=\frac{3}{5}$-----（12分）

点评 本题考查独立性检验知识的运用，考查分层抽样，考查概率知识，考查学生分析解决问题的能力，确定基本事件总数是关键．