题目内容
在区间(0,
)上随机取一个数x,则事件“tanxcosx≥
”发生的概率为( )
| π |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:先化简不等式,确定满足tanx•cosx≥
且在区间(0,
)内x的范围,根据几何概型利用长度之比可得结论.
| 1 |
| 2 |
| π |
| 2 |
解答:
解:∵tanx•cosx≥
,即sinx≥
且cosx≠0,
∵x∈(0,
),
∴x∈[
,
),
∴在区间(0,
)内,满足tanx•cosx≥
发生的概率为P=
=
.
故选:D
| 1 |
| 2 |
| 1 |
| 2 |
∵x∈(0,
| π |
| 2 |
∴x∈[
| π |
| 6 |
| π |
| 2 |
∴在区间(0,
| π |
| 2 |
| 1 |
| 2 |
| ||||
|
| 2 |
| 3 |
故选:D
点评:本题考查几何概型,三角函数的化简,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知全集U={1,2,3,4,5},其子集A={1,3},B={3,5},求(∁UA)∪∁UB=( )
| A、{1,3,5} |
| B、{2,4,5} |
| C、{1,3,4} |
| D、{1,2,4,5} |
函数f(x)=sinx在区间[a,b]上是增函数,且f(a)=-1,f(b)=1,则cos
的值为( )
| a+b |
| 2 |
| A、-1 | ||||
| B、0 | ||||
C、
| ||||
| D、1 |
由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割试判断,对于任一戴德金分割(M,N),下列选项中,不可能成 立的是( )
| A、M没有最大元素,N有一个最小元素 |
| B、M没有最大元素,N也没有最小元素 |
| C、M有一个最大元素,N有一个最小元素 |
| D、M有一个最大元素,N没有最小元素 |
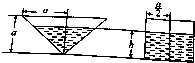 一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图,两容器盛有液体的体积正好相等,且液面高均为h,求h.
一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图,两容器盛有液体的体积正好相等,且液面高均为h,求h.