题目内容
一个几何体的三视图如图所示，则几何体的体积为 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个以正视图为底面的棱柱，计算出底面面积和高，代入柱体体积公式，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个以正视图为底面的棱柱，
棱柱的底面面积S=（2.4+0.6）×2=6，
棱柱的高h=2，
故棱柱的体积V=Sh=12，
故答案为：12
棱柱的底面面积S=（2.4+0.6）×2=6，
棱柱的高h=2，
故棱柱的体积V=Sh=12，
故答案为：12
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
直线x-y+3=0的倾斜角是（ ）
| A、30° | B、45° |
| C、60° | D、135° |
设复数z满足z•（1-i）=2，则复数z的模|z|等于（ ）
A、
| ||
| B、2 | ||
C、
| ||
| D、4 |
在区间（0，
）上随机取一个数x，则事件“tanxcosx≥
”发生的概率为（ ）
| π |
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
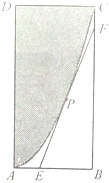如图，有一个长方形地块ABCD，边AB为2km，AD为4km．，地块的一角是湿地（图中阴影部分），其边缘线AC是以直线AD为对称轴，以A为顶点的抛物线的一部分．现要铺设一条过边缘线AC上一点P的直线型隔离带EF，E，F分别在边AB，BC上（隔离带不能穿越湿地，且占地面积忽略不计）．设点P到边AD的距离为t（单位：km），△BEF的面积为S（单位：km2）．