题目内容
4.已知函数f(x)=x3+x,g(x)=ln(x+1)+$\frac{a{x}^{2}+ax-1}{x+1}$,其中a≥-$\frac{5}{16}$.(Ⅰ)对任意实数a,b,c,满足a+b,b+c,c+a都是非负数,判断f(a)+f(b)+f(c)的正负号,并证明你的结论;
(Ⅱ)若对任意的x1∈[1,3],存在x2∈[1,3],使得f(x1)≥g(x2)成立,求a的取值范围;
(Ⅲ)是否存在实数a,对任意的x1,x2∈[1,3]都有f(x1)≥g(x2)成立?若存在,求出a的取值范围;若不存在,请说明理由.
分析 (Ⅰ)根据函数f(x)的单调性以及奇偶性得到f(a)+f(b)≥0,f(b)+f(c)≥0,f(c)+f(a)≥0,相加即可;
(Ⅱ)问题等价于f(x)min≥g(x)min,根据函数的单调性分别求出f(x)和g(x)的最小值jk;
(Ⅲ)问题等价于f(x)min≥g(x)max,分别求出f(x)的最小值和g(x)的最大值,求出a的范围即可.
解答 解:(Ⅰ)容易证明函数f(x)=x3+x是递增的奇函数,
而a+b≥0,b+c≥0,c+a≥0,则a≥-b,b≥-c,c≥-a,
∴f(a)≥f(-b),f(b)≥f(-c),f(c)≥f(-a),
即f(a)+f(b)≥0,f(b)+f(c)≥0,f(c)+f(a)≥0,
三式相加的f(a)+f(b)+f(c)≥0,
∴f(a)+f(b)+f(c)非负.
(Ⅱ)g′(x)=${(\frac{1}{x+1}+\frac{1}{2})}^{2}$+a-$\frac{1}{4}$,
而$\frac{1}{x+1}$∈[$\frac{1}{4}$,$\frac{1}{2}$],∴g′(x)∈[a+$\frac{5}{16}$,a+$\frac{3}{4}$],
又a≥-$\frac{5}{16}$,∴g′(x)≥0恒成立.
对任意的x1∈[1,3],存在x2∈[1,3],使得f(x1)≥g(x2)成立”等价于f(x)min≥g(x)min,
∵f(x)=x3+x在[1,3]上是单调递增函数,
∴f(x)min=f(1)=2,
而g(x)在[1,3]上单调递增函数,
∴g(x)min=g(1)=a+ln2-$\frac{1}{2}$,
由f(x)min≥g(x)min,得-$\frac{5}{16}$≤a≤$\frac{5}{2}$-ln2.
(Ⅲ)“对任意的x1,x2∈[1,3]都有f(x1)≥g(x2)成立”等价于f(x)min≥g(x)max,
而f(x)min=f(1)=2,g(x)max=g(3)=3a+2ln2-$\frac{1}{4}$,
故$\left\{\begin{array}{l}{a≥-\frac{5}{16}}\\{a≤-\frac{2}{3}ln2+\frac{3}{4}}\end{array}\right.$,解得:-$\frac{5}{16}$≤a≤-$\frac{2}{3}$ln2+$\frac{3}{4}$,
∴满足条件的a存在,取值范围为-$\frac{5}{16}$≤a≤-$\frac{2}{3}$ln2+$\frac{3}{4}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,函数恒成立问题,是一道中档题.

| A. | 不存在x0∈R+,使log2x0>0 | B. | 对任意的x∈R+,有log2x>0 | ||
| C. | 对任意的x∈R+,有log2x≤0 | D. | 存在x0∈R+,使log2x0>0 |
| 组别 | [65,75) | [75,85) | [85,95) | [95,105) | [105,115) | [115,150) |
| 频数 | 3 | 4 | 13 | 15 | 10 | 5 |
(1)在这50名参考人员中任取一位,求分数不低于105分的概率;
(2)为了进一步了解这些参考人员的得分情况,再从分数在[65,75)的参考人员A,B,C中选出2位,从分数在[115,150)中的参考人员D,E,F,G,H中选出1位进行研究,求A和D同时被选到的概率.
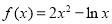 在其定义域的一个子区间
在其定义域的一个子区间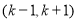 内不是单调函数,则实数
内不是单调函数,则实数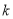 的取值范围是( )
的取值范围是( )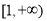 B.
B.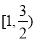 C.
C. D.
D.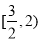
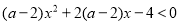 对一切
对一切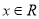 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )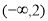 B.[-2,2] C.(-2,2] D.
B.[-2,2] C.(-2,2] D.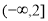
 的是( )
的是( )


