题目内容
16.先后抛掷一枚质地均匀的骰子,得到的点数分别为a,b,那么2a≥5b的概率是$\frac{1}{6}$.分析 由a≥$\frac{5}{2}$b,符合条件的结果数有六个,再计算出所有的结果数,由公式计算出正确答案.
解答 解:总的基本事件数是6×6=36,满足2a≥5b,即a≥$\frac{5}{2}$b的基本事件:
b=1,a有4种情况;b=2,a有2种情况,共6种情况;
∴2a≥5b的概率是$\frac{6}{36}$=$\frac{1}{6}$,
故答案为$\frac{1}{6}$.
点评 本题考查等可能事件的概率,解题的关键是理解事件“a≥$\frac{5}{2}$b”,求出它所包含的基本事件数,概率解题,研究清楚事件的性质很重要.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.函数f(x)=$\left\{\begin{array}{l}{lnx(x>0)}\\{-\sqrt{-x}(x≤0)}\end{array}\right.$与g(x)=$\frac{1}{2}$(|x+a|+1)的图象上存在关于y轴对称的点,则实数a的取值范围是( )
| A. | (-∞,3-2ln2] | B. | [3-2ln2,+∞) | C. | [$\sqrt{e}$,+∞) | D. | (-∞,$-\sqrt{e}$] |
1.锐角三角形△ABC中,若A=2B,则下列叙述正确的是( )
①sin3B=sinC
②$tan\frac{3B}{2}tan\frac{C}{2}=1$
③$\frac{π}{6}<B<\frac{π}{4}$
④$\frac{a}{b}∈({\sqrt{3},2})$.
①sin3B=sinC
②$tan\frac{3B}{2}tan\frac{C}{2}=1$
③$\frac{π}{6}<B<\frac{π}{4}$
④$\frac{a}{b}∈({\sqrt{3},2})$.
| A. | ①② | B. | ①②③ | C. | ③④ | D. | ①④ |
6.小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为( )
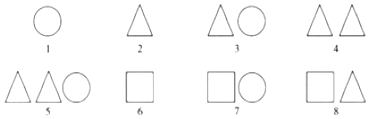

| A. | 670 | B. | 672 | C. | 335 | D. | 336 |
 满足
满足 ,数列
,数列 是等比数列,且
是等比数列,且 , 则
, 则 的值等于 .
的值等于 .