题目内容
1.小型风力发电项目投资较少,开发前景广阔.受风力自然资源影响,项目投资存在一定风险.根据测算,IEC(国际电工委员会)风能风区的分类标准如下:| 风能分类 | 一类风区 | 二类风区 |
| 平均风速m/s | 8.5---10 | 6.5---8.5 |
(Ⅰ)记投资A,B项目的利润分别为ξ和η,试写出随机变量ξ与η的分布列和期望Eξ,Eη;
(Ⅱ)根据以上的条件和市场调研,试估计一年后两个项目的平均利润之和z=Eξ+Eη的最大值,并据此给出公司分配投资金额建议.
分析 (1)先求出A项目投资利润ξ的分布列,从而能求出Eξ,再求出B项目投资利润η的分布列,从而能求出Eη.
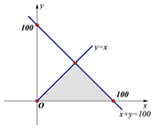
(2)z=Eξ+Eη=0.16x+0.19y,利用$\left\{\begin{array}{l}{x+y≤100}\\{x≥y}\\{x,y≥0}\end{array}$,作出可行域,由此能求出当x=50,y=50,公司获得获利最大,最大为17.5万元,从而建议给两公司各投资50万.
解答 (本题满分为12分)
解:(1)A项目投资利润ξ的分布列
| ξ | 0.4x | -0.2x |
| P | 0.6 | 0.4 |
B项目投资利润η的分布列:
| η | 0.35y | -0.1y | 0 |
| P | 0.6 | 0.2 | 0.2 |
 Eη=0.21y-0.02y=0.19y
Eη=0.21y-0.02y=0.19y(2)z=Eξ+Eη=0.16x+0.19y
而$\left\{\begin{array}{l}{x+y≤100}\\{x≥y}\\{x,y≥0}\end{array}$,作出可行域如右图,
由图可知,当x=50,y=50,公司获得获利最大,最大为17.5万元.
故建议给两公司各投资50万.
点评 本题考查离散型随机变量的分布列、数学期望的求法及应用,考查离散型随机变量的分布列和数学期望、线性规划等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

练习册系列答案
相关题目
12.△ABC的三个内角A、B、C,所对的边分别是a、b、c,若a=2,c=2$\sqrt{3}$,tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB,则△ABC的面积S△ABC=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
16.已知x,y∈R,下列不等式不能恒成立的是( )
| A. | |x|≥0 | B. | x2-2x-3≥0 | C. | 2x>0 | D. | x2+y2≥2xy |
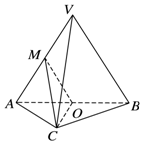 如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.
如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.