题目内容
4.某矿业公司对A、B两个铁矿项目调研结果是:A项目获利40%的可能性为0.6,亏损20%的可能性为0.4;B项目获利35%的可能性为0.6,亏损10%的可能性为0.2,不赔不赚的可能性为0.2.现计划用不超过100万元的资金投资A、B两个项目,假设投资A项目的资金为x(x≥0)万元,投资B项目的资金为y(y≥0)万元,且公司要求对A项目的投资不得低于B项目.(1)请根据公司投资限制条件,写出x,y满足的条件,并将它们表示在平面xOy内;
(2)记投资A、B项目的利润分别为M和N,试写出随机变量M与N的分布列和期望E(M),E(N);
(3)根据(1)的条件和调研结果,试估计两个项目的平均利润之和z=E(M)+E(N)的最大值.
分析 (1)根据公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目,公司要求对A项目的投资不得低于B项目,可得x,y满足的条件,从而可得平面区域;
(2)利用未来一年内,位于一类风区的A项目获利40%的可能性为0.6,亏损20%的可能性为0.4;B项目位于二类风区,获利35%的可能性为0.6,亏损10%的可能性是0.2,不赔不赚的可能性是0.2,可得随机变量ξ与η的分布列和期望Eξ,Eη;
(3)利用平面区域,即可求得一年后两个项目的平均利润之和z=Eξ+Eη的最大值
解答  解:(Ⅰ)由题意,公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目,公司要求对A项目的投资不得低于B项目可得$\left\{\begin{array}{l}{x+y≤100}\\{x≥y}\\{x≥0,y≥0}\end{array}\right.$,
解:(Ⅰ)由题意,公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目,公司要求对A项目的投资不得低于B项目可得$\left\{\begin{array}{l}{x+y≤100}\\{x≥y}\\{x≥0,y≥0}\end{array}\right.$,
表示的区域如图所示;
(Ⅱ)随机变量ξ的分布列为
| M | 0.4x | -0.2x |
| P | 0.6 | 0.4 |
随机变量η的分布列为
| N | 0.35y | -0.1y | 0 |
| P | 0.6 | 0.2 | 0.2 |
(Ⅲ)z=EM+EN=0.16x+0.19y,$\left\{\begin{array}{l}{x+y=100}\\{x=y}\end{array}\right.$,可得x=y=50,
根据图象,可得x=y=50时,估计一年后两个项目的平均利润之和z=EM+EN的最大值为17.5万元.
点评 本题考查线性规划知识,考查随机变量ξ与η的分布列和期望,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
14.下列函数中,在定义域上为减函数的是( )
| A. | y=x2 | B. | y=cosx | C. | $y={x^{\frac{1}{2}}}$ | D. | y=-lnx |
1.小型风力发电项目投资较少,开发前景广阔.受风力自然资源影响,项目投资存在一定风险.根据测算,IEC(国际电工委员会)风能风区的分类标准如下:
某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是:未来一年内,位于一类风区的A项目获利40%的可能性为0.6,亏损20%的可能性为0.4; B项目位于二类风区,获利35%的可能性为0.6,亏损10%的可能性是0.2,不赔不赚的可能性是0.2.假设投资A项目的资金为x(x≥0)万元,投资B项目资金为y(y≥0)万元,且公司要求对A项目的投资不得低于B项目.
(Ⅰ)记投资A,B项目的利润分别为ξ和η,试写出随机变量ξ与η的分布列和期望Eξ,Eη;
(Ⅱ)根据以上的条件和市场调研,试估计一年后两个项目的平均利润之和z=Eξ+Eη的最大值,并据此给出公司分配投资金额建议.
| 风能分类 | 一类风区 | 二类风区 |
| 平均风速m/s | 8.5---10 | 6.5---8.5 |
(Ⅰ)记投资A,B项目的利润分别为ξ和η,试写出随机变量ξ与η的分布列和期望Eξ,Eη;
(Ⅱ)根据以上的条件和市场调研,试估计一年后两个项目的平均利润之和z=Eξ+Eη的最大值,并据此给出公司分配投资金额建议.
14.观察下列(如图)数表规律,则数2007的箭头方向是( )


| A. |  | B. |  | C. |  | D. |  |
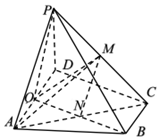 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.