题目内容
已知椭圆的焦点是F1(-1,0),F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等差中项.若点P在第三象限,且∠PF1F2=120°,则sin∠F1PF2= .
考点:椭圆的简单性质
专题:解三角形,圆锥曲线的定义、性质与方程
分析:首先根据题意建立|PF1|+|PF2|=2|F1F2|=4,进一步在三角形中,利用余弦定理求出|PF1|=
,|PF2|=
,最后利用正弦定理求出结果.
| 6 |
| 5 |
| 14 |
| 5 |
解答:
解:椭圆的焦点是F1(-1,0),F2(1,0),
则:|F1F2|=2
又P为椭圆上一点,且|F1F2|是的等差中项
|PF1|+|PF2|=2|F1F2|=4 ①
在△PF1F2中,∠PF1F2=120°
利用余弦定理得:|PF2|2=|PF1|2+|F1F2|2-2|PF1||F1F2|COS120°②
由①②解得:|PF2|=
|PF1|=
利用正弦定理:
=
解得:sin∠F1PF2=
故答案为:
则:|F1F2|=2
又P为椭圆上一点,且|F1F2|是的等差中项
|PF1|+|PF2|=2|F1F2|=4 ①
在△PF1F2中,∠PF1F2=120°
利用余弦定理得:|PF2|2=|PF1|2+|F1F2|2-2|PF1||F1F2|COS120°②
由①②解得:|PF2|=
| 14 |
| 5 |
| 6 |
| 5 |
利用正弦定理:
| |F1F2| |
| sin∠F1PF2 |
| |PF2| |
| sin∠PF1F2 |
解得:sin∠F1PF2=
5
| ||
| 14 |
故答案为:
5
| ||
| 14 |
点评:本题考查的知识要点:椭圆的定义,等差中项的应用,正弦定理的应用和余弦定理得应用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
复数1+
在复平面上对应的点的在( )
| 1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数f(x)=x(x2-1)的图象大致是( )
A、 |
B、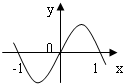 |
C、 |
D、 |
函数y=a-x2+4x(a>1)的单调递增区间是( )
| A、(2,+∞) |
| B、(-2,+∞) |
| C、(-∞,-2) |
| D、(-∞,2) |
下列说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| C、命题“a、b都是有理数”的否定是“a、b都不是有理数” |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
设{an}是任意等比数列,它的前n项和,前2n项和与前3n项分别为X,Y,Z,则下列等式中恒成立的是( )
| A、X+Z=2Y |
| B、Y(Y-X)=Z(Z-X) |
| C、Y2=XZ |
| D、Y(Y-X)=X(Z-X) |