题目内容
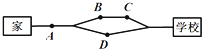 小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是
小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是| 1 |
| 3 |
(1)求小明没有遇到红灯的概率;
(2)记小明等候的总时间为ξ,求ξ的分布列并求数学期望E(ξ).
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(I)记“小明没有遇到红灯”为事件A,利用相互独立事件的概率乘法公式能求出小明没有遇到红灯的概率.
(II)由题可知:ξ=0,10,20,30,分别求出相对应的概率,由此能求出ξ的分布列并求数学期望.
(II)由题可知:ξ=0,10,20,30,分别求出相对应的概率,由此能求出ξ的分布列并求数学期望.
解答:
解:(I)记“小明没有遇到红灯”为事件A,
则P(A)=
×(1-
)3+
×(1-
)2=
…(4分)
(II)由题可知:ξ=0,10,20,30 …(6分)
P(ξ=0)=
,
P(ξ=10)=
(1-
)2+
(1-
)=
…(8分)
P(ξ=20)=
(
)2(1-
)+
(
)2=
…(10分)
P(ξ=30)=
(
)3=
…(12分)
∴ξ的分布列:
∴E(ξ)=0×
+10×
+20×
+30×
=
…(14分)
则P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 10 |
| 27 |
(II)由题可知:ξ=0,10,20,30 …(6分)
P(ξ=0)=
| 10 |
| 27 |
P(ξ=10)=
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
P(ξ=20)=
| 1 |
| 2 |
| C | 2 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 3 |
| 1 |
| 6 |
P(ξ=30)=
| 1 |
| 2 |
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 54 |
∴ξ的分布列:
| 0 | 10 | 20 | 30 | |||||||||
| P |
|
|
|
|
| 10 |
| 27 |
| 4 |
| 9 |
| 1 |
| 6 |
| 1 |
| 54 |
| 25 |
| 3 |
点评:本题考查概率的计算,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
从1,2,3,4,5,6这六个数中,每次取出两个不同的数记为a,b,则共可得到2
的不同值的个数是( )
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
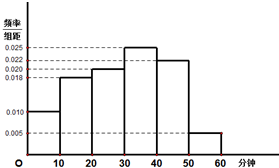 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图;将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.